
分析 (I)求导f′(x)=ex+m,从而讨论m以确定导数的正负,从而确定函数的单调性;
(II)当m=-1时,g(x)=-x+lnx,(x>0);再求导g′(x)=-1+$\frac{1}{x}$,从而求得|g(x)|≥1;再令h(x)=$\frac{lnx}{x}$$+\frac{1}{2}$,则h′(x)=$\frac{1-lnx}{{x}^{2}}$;从而求得h(x)≤h(e)=$\frac{1}{e}$$+\frac{1}{2}$<1;从而判断.
解答 解:(I)∵f(x)=ex+mx-2,
∴f′(x)=ex+m,
当m≥0时,f′(x)>0;
函数f(x)的单调增区间为R;
当m<0时,由f′(x)>0解得,x>ln(-m);
由f′(x)<0解得,x<ln(-m);
故函数f(x)的单调增区间为[ln(-m),+∞),
单调减区间为(-∞,ln(-m));
(II)当m=-1时,g(x)=-x+lnx,(x>0);
g′(x)=-1+$\frac{1}{x}$,
故g(x)在x=1处取得极大值,
故g(x)≤g(1)=-1;
故|g(x)|≥1;
令h(x)=$\frac{lnx}{x}$$+\frac{1}{2}$,则h′(x)=$\frac{1-lnx}{{x}^{2}}$;
故h(x)在(0,e)上是增函数,在(e,+∞)上是减函数;
故h(x)在x=e处取得最大值;
∴h(x)≤h(e)=$\frac{1}{e}$$+\frac{1}{2}$<1;
故方程$|{g(x)}|=\frac{lnx}{x}+\frac{1}{2}$没有实数解.
点评 本题考查了方程的根与函数的关系应用及导数的综合应用,同时考查了分类讨论的思想应用,属于中档题.


科目:高中数学 来源: 题型:选择题
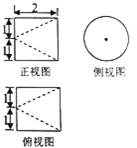
| A. | $\frac{π}{3}$cm3 | B. | $\frac{2π}{3}$cm3 | C. | πcm3 | D. | $\frac{4π}{3}$cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 甲、乙两名同学8次数学测验成绩如茎叶图所示,$\overline{x}$1,$\overline{x}$2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1,s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有( )
甲、乙两名同学8次数学测验成绩如茎叶图所示,$\overline{x}$1,$\overline{x}$2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1,s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有( )| A. | $\overline{x}$1>$\overline{x}$2,s1<s2 | B. | $\overline{x}$1=$\overline{x}$2,s1<s2 | C. | $\overline{x}$1=$\overline{x}$2,s1=s2 | D. | $\overline{x}$1<$\overline{x}$2,s1>s2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
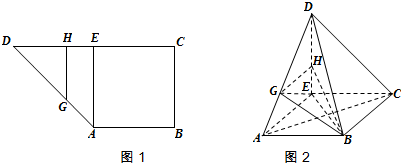
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图直方图:
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图直方图:| 是否近视 年级名次 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com