
分析 (1)先求导,再分离参数,利用基本不等式即可求出a的范围;
(2)根据零点即是导数等于0时的方程的根,根据根与系数的关系得到x1x2=1,化简整理f(x1)+f(x2),再根据做差法比较大小,需要构造函数g(x)=x-lnx-1,利用导数求出函数的最小值,问题得以证明.
解答 解:(1)∵f(x)在(0,+∞)上是增函数,
∴f′(x)=$\frac{2}{x}$+$\frac{a}{{(x+1)}^{2}}$≥0恒成立,
∴a≥-$\frac{{2(x+1)}^{2}}{x}$=-2(x+$\frac{1}{x}$+2),
∵x+$\frac{1}{x}$+2≥2$\sqrt{x•\frac{1}{x}}$+2=4,当且仅当x=1时取等号,
∴a≥-8,
故a的取范围为[-8,+∞);
(2)由(1)知f′(x)=$\frac{2}{x}$+$\frac{a}{{(x+1)}^{2}}$,
令f′(x)=0,
得到2x2+(a+4)x+2=0,
由题意得x1,x2是方程的两根,则x1x2=1,
∴f(x1)+f(x2)
=2lnx1+$\frac{{ax}_{1}}{{x}_{1}+1}$+2lnx2+$\frac{{ax}_{2}}{{x}_{2}+1}$
=2lnx1x2+$\frac{{ax}_{1}}{{x}_{1}+1}$+$\frac{{ax}_{2}}{{x}_{2}+1}$
=a•$\frac{2{+x}_{1}{+x}_{2}}{2{+x}_{1}{+x}_{2}}$=a,
∴$\frac{f({x}_{1})+f({x}_{2})}{x+1}$-$\frac{f(x)-2x+2}{x}$
=$\frac{a}{x+1}$-$\frac{2lnx+\frac{ax}{x+1}-2x+2}{x}$
=$\frac{2(x-1)-2lnx}{x}$,
设g(x)=2(x-lnx-1),
则g′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$,
当g′(x)<0时,即0<x<1,在g(x)在(0,1)上单调递减,
当g′(x)>0时,即x>1,在g(x)在(1,+∞)上单调递增,
∴g(x)min=g(1)=0,
∴当x∈(0,+∞)时,x-lnx-1>0,
故$\frac{f({x}_{1})+f({x}_{2})}{x+1}$≥$\frac{f(x)-2x+2}{x}$,当且仅当x=1时取等号.
点评 本题考查了导数的几何意义以及导数和函数的最值的关系,以及函数恒成立,不等式的证明等问题,考查了转化能力,运算能力,属于难题.


科目:高中数学 来源: 题型:解答题
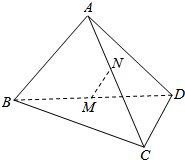 如图,空间四边形ABCD各边边长均为a,M,N分别是对角线BD,AC的中点.
如图,空间四边形ABCD各边边长均为a,M,N分别是对角线BD,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
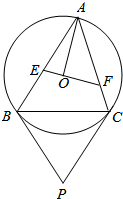 如图,锐角△ABC内接于圆0.过圆心0且垂直于半径0A的直线分别交边AB、AC于点E、F.设圆0在B、C两点处的切线相交于点P.求证:直线AP平分线段EF.
如图,锐角△ABC内接于圆0.过圆心0且垂直于半径0A的直线分别交边AB、AC于点E、F.设圆0在B、C两点处的切线相交于点P.求证:直线AP平分线段EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com