
【题目】设椭圆![]() 的左顶点为
的左顶点为![]() ,右顶点为
,右顶点为![]() ,已知椭圆
,已知椭圆![]() 的离心率为
的离心率为![]() ,且以线段
,且以线段![]() 为直径的圆被直线
为直径的圆被直线![]() 所截的弦长为
所截的弦长为![]() .
.
(1)求椭圆的方程;
(2)记椭圆![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线交椭圆于
的直线交椭圆于![]() 两点.若线段
两点.若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(x+1).
(1)若0<f(1-2x)-f(x)<1,求实数x的取值范围;
(2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,有g(x)=f(x),当x∈[1,2]时,求函数y=g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 上顶点为A,右焦点为F,直线
上顶点为A,右焦点为F,直线![]() 与圆
与圆![]() 相切,其中
相切,其中![]() .
.
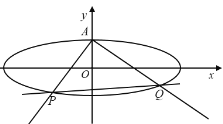
(1)求椭圆的方程;
(2)不过点A的动直线l与椭圆C相交于P,Q两点,且![]() ,证明:动直线l过定点,并且求出该定点坐标.
,证明:动直线l过定点,并且求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下统计表和分布图取自《清华大学2019年毕业生就业质量报告》.

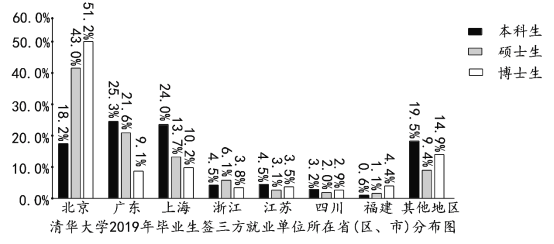
则下列选项错误的是( )
A.清华大学2019年毕业生中,大多数本科生选择继续深造,大多数硕士生选择就业
B.清华大学2019年毕业生中,硕士生的就业率比本科生高
C.清华大学2019年签三方就业的毕业生中,本科生的就业城市比硕士生的就业城市分散
D.清华大学2019年签三方就业的毕业生中,留北京人数超过一半
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com