
(本小题满分14分)
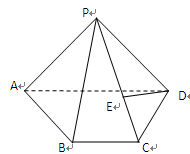
如图,在三棱锥P-ABC中,底面△ABC为等边三角形,∠APC=90°,PB=AC=2PA=4,O为AC的中点。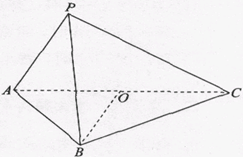
(Ⅰ)求证:BO⊥PA;
(Ⅱ)判断在线段AC上是否存在点Q(与点O不重合),使得△PQB为直角三角形?若存在,试找出一个点Q,并求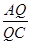 的值;若不存在,说明理由。
的值;若不存在,说明理由。
(Ⅰ)在等边△ABC中BO⊥AC,BO=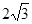 ,在直角△PAC中PO=2,在△PBO中,由PB=4,得PB2=PO2+BO2所以BO⊥PO所以BO⊥平面PAC所以BO⊥PA(Ⅱ)线段AC上存在点Q, 满足
,在直角△PAC中PO=2,在△PBO中,由PB=4,得PB2=PO2+BO2所以BO⊥PO所以BO⊥平面PAC所以BO⊥PA(Ⅱ)线段AC上存在点Q, 满足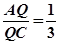 使得△PQB为直角三角形
使得△PQB为直角三角形
解析试题分析:(Ⅰ)证明:如图,连结PO,
在等边△ABC中,因为O是AC的中点,且AC=4,
所以BO⊥AC,BO=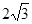 。
。
在直角△PAC中,因为O是斜边AC的中点,且AC=4,
所以PO=2,
在△PBO中,由PB=4,得PB2=PO2+BO2,
所以BO⊥PO。 3分
又因为AC∩PO=O,AC 平面PAC,PO
平面PAC,PO 平面PAC,
平面PAC,
所以BO⊥平面PAC, 5分
又因为PA 平面PAC,
平面PAC,
所以BO⊥PA。 7分
(Ⅱ)答:线段AC上存在点Q,使得△PQB为直角三角形。
具体过程如下:
如图,过P作PM⊥AC于点M,连结BM,
因为BO⊥平面PAC,
所以BO⊥PM。
又因为BO∩AC=O,BO 平面ABC,AC
平面ABC,AC 平面ABC,
平面ABC,
所以PM⊥平面ABC, 10分
所以PM⊥BM,即△PMB为直角三角形。
故当点Q与点M重合时,△PQB为直角三角形。 12分
在直角△PAC中,由∠APC=90°,AC=2PA=4,
得AM=1,(即AQ=1),MC=3(即QC=3),
所以当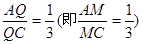 时,△PQB为直角三角形。 14分
时,△PQB为直角三角形。 14分
考点:线线垂直线面垂直的判定和性质
点评:线线垂直与线面垂直之间可以互为条件结论,本题主要利用两者间的互相推出关系证明计算


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分.
如图已知四棱锥 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱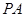 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点 分别是
分别是 的中点.求
的中点.求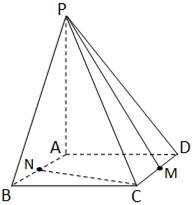
(1)异面直线 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)四棱锥 的表面积.
的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正方形 所在平面与平面四边形
所在平面与平面四边形 所在平面互相垂直,△
所在平面互相垂直,△ 是等腰直角三角形,
是等腰直角三角形,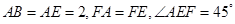
(1)线段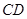 的中点为
的中点为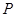 ,线段
,线段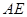 的中点为
的中点为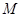 ,求证:
,求证: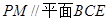 ;
;
(2)求直线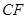 与平面
与平面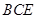 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
四棱锥 ,面
,面 ⊥面
⊥面 .侧面
.侧面 是以
是以 为直角顶点的等腰直角三角形,底面
为直角顶点的等腰直角三角形,底面 为直角梯形,
为直角梯形, ,
,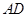 ∥
∥ ,
, ⊥
⊥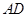 ,
, 为
为 上一点,且
上一点,且 .
.
(Ⅰ)求证 ⊥
⊥ ;
;
(Ⅱ)求二面角 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)如图,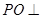 平面
平面 ,点
,点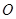 在
在 上,
上,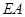 ∥
∥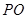 ,四边形
,四边形 为直角梯形,
为直角梯形,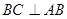 ,
, ,
,

(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)直线 上是否存在点
上是否存在点 ,使
,使 ∥平面
∥平面 ,若存在,求出点
,若存在,求出点 ;若不存在,说明理由。
;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
在正四棱锥V - ABCD中,P,Q分别为棱VB,VD的中点, 点M在边BC上,且BM: BC = 1 : 3,AB =2 ,VA =" 6."
,VA =" 6." 
(I )求证CQ∥平面PAN;
(II)求证:CQ⊥AP.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
如图,在直三棱柱ABC-A1B1C1中, ,
, ,
,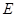 是
是 的中点,
的中点, 是
是 中点.
中点.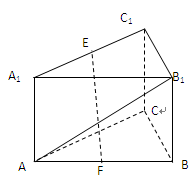
(1)求证: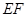 ∥面
∥面 ;
;
(2)求直线EF与直线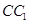 所成角的正切值;
所成角的正切值;
(3)设二面角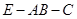 的平面角为
的平面角为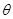 ,求
,求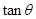 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,在四棱锥S - ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA ="AB=BC" =2,AD =1.M是棱SB的中点.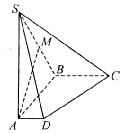
(Ⅰ)求证:AM∥面SCD;
(Ⅱ)求面SCD与面SAB所成二面角的余弦值;
(Ⅲ)设点N是直线CD上的动点,MN与面SAB所成的角为 ,求sin
,求sin 的最大值,
的最大值,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com