
(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分.
如图已知四棱锥 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱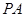 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点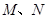 分别是
分别是 的中点.求
的中点.求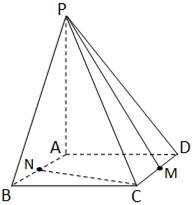
(1)异面直线 与
与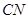 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)四棱锥 的表面积.
的表面积.
(1) .(2) 144
.(2) 144
解析试题分析:
(1)解法 一:连结 ,可证
,可证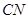 ∥
∥ ,直线
,直线 与
与 所成角等于直线
所成角等于直线 与
与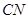 所成角.因为
所成角.因为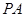 垂直于底面,所以
垂直于底面,所以 ,点
,点 分别是
分别是 的中点,
的中点, 
 ,在
,在 中,
中, ,
, ,
, ,
,
即异面直线 与
与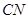 所成角的大小为
所成角的大小为 .
.
解法二:以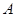 为坐标原点建立空间直角坐标系可得
为坐标原点建立空间直角坐标系可得 ,
, ,
, ,
, ,
, ,
,
直线 与
与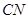 所成角为
所成角为 ,向量
,向量 的夹角为
的夹角为

又 ,
, ,
,
即异面直线 与
与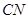 所成角的大小为
所成角的大小为 .
.
(说明:两种方法难度相当)
(2) 因为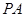 垂直于底面,所以
垂直于底面,所以 ,
, 即
即 ≌
≌
 ,同理
,同理
 ≌
≌ …………8分
…………8分
底面四边形 是边长为6的正方形,所以
是边长为6的正方形,所以
又





所以四棱锥 的表面积是144
的表面积是144
考点:本题考查了异面直线的夹角及四棱锥表面积的求法
点评:高考中的立体几何问题主要是探求和证明空间几何体中的平行和垂直关系以及空间角、体积等计算问题.对于平行和垂直问题的证明或探求,其关键是把线线、线面、面面之间的关系进行灵活的转化.在寻找解题思路时,不妨采用分析法,从要求证的结论逐步逆推到已知条件


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:解答题
如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,且AB=AD,BC=DC.
(1)求证: 平面EFGH;
平面EFGH;
(2)求证:四边形EFGH是矩形.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,已知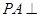 ⊙
⊙ 所在的平面,AB是⊙
所在的平面,AB是⊙ 的直径,
的直径,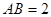 ,
, 是⊙
是⊙ 上一点,且
上一点,且 ,
,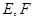 分别为
分别为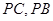 中点。
中点。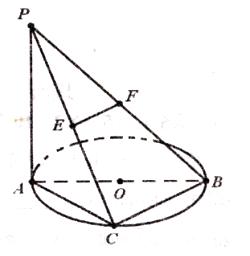
(1)求证: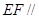 平面
平面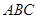 ;
;
(2)求证: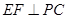 ;
;
(3)求三棱锥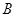 -
-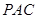 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
如图,在三棱锥P-ABC中,底面△ABC为等边三角形,∠APC=90°,PB=AC=2PA=4,O为AC的中点。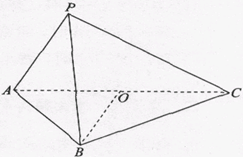
(Ⅰ)求证:BO⊥PA;
(Ⅱ)判断在线段AC上是否存在点Q(与点O不重合),使得△PQB为直角三角形?若存在,试找出一个点Q,并求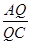 的值;若不存在,说明理由。
的值;若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com