
分析 (Ⅰ)通过讨论x的范围求出各个区间上的不等式的解集,取并集即可;
(Ⅱ)问题等价于fmin(x)≤-5,求出f(x)的最小值,得到关于t的不等式,解出即可.
解答 解:(Ⅰ)原不等式可化为$\left\{\begin{array}{l}x>\frac{3}{2}\\ 2x+1-2x+3<1\end{array}\right.$或$\left\{\begin{array}{l}{-\frac{1}{2}≤x≤\frac{3}{2}}\\{2x+1+2x-3<1}\end{array}\right.$或$\left\{\begin{array}{l}{x<-\frac{1}{2}}\\{-2x-1+2x-3<1}\end{array}\right.$..(3分)
解得x∈∅或$-\frac{1}{2}≤x<\frac{3}{4}$或$x<-\frac{1}{2}$…(4分)
综上,原不等式的解集是$\left\{{x\left|{x<\frac{3}{4}}\right.}\right\}$…(5分)
(Ⅱ)解:?x∈R,使f(x)≤-5,
等价于fmin(x)≤-5…(6分)
∵|f(x)|=||2x+1|-|2x-t||≤|(2x+1)-(2x-t)|=|1+t|…(7分)
∴-|1+t|≤f(x)≤|1+t|,
所以f(x)取得最小值-|1+t|…(8分)
∴-|1+t|≤-5,
得t≥4或t≤-6,
∴t的取值范围是(-∞,-6]∪[4,+∞)…(10分)
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ±1 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
| 男性驾驶员人数 | |||
| 女性驾驶员人数 | |||
| 合计 | |||
| P(K2≥k0) | 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
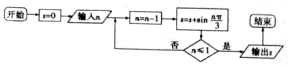
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-∞,1) | C. | (0,+∞) | D. | $(-∞,\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
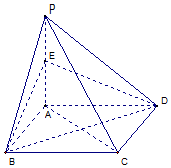 如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.
如图,点P为矩形ABCD所在平面外一点,PA⊥平面ABCD,点E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com