考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件推导出
a1=(a1+2)2,a
n+1-a
n=4,由此能求出a
n=4n-2.
(2)①要证对任意的n∈N
*,都有b
n∈A,只要证:对任意的n∈N
*,存在m∈N
*,使得3
n-1+1=2m.
②由已知条件得2×3
n-1=4r-2,由此求出T
n=3
n-1,从而能求出
的值.
解答:
本题满分(20分),第1小题满分(10分),第2小题满分(10分)
(1)解:由题意
=
,a
n>0,得S
n=
(a
n+2)
2,
当n=1时,
a1=(a1+2)2,解得a
1=2,(2分)
当n≥2时,S
n+1=
(a
n+1+2)
2.
∴a
n+1=S
n+1-S
n=
[(an+1+2)2-(an+2)2],
整理,得(a
n+1+a
n)(a
n+1-a
n-4)=0.(4分)
由题意知a
n+1+a
n≠0,∴a
n+1-a
n=4.(2分)
∴数列{a
n}为首项为2,公差为4的等差数列,即a
n=4n-2.(2分)
(2)①证明:要证对任意的n∈N
*,都有b
n∈A,
只要证:对任意的n∈N
*,存在m∈N
*,使得2×3
n-1=4m-2,即3
n-1+1=2m.
∵3
n-1是奇数,∴3
n-1+1为偶数,(2分)
∴存在正整数m=
,使得2×3
n-1=4m-2.(3分)
∴数列{b
n}中的所有项都在数列{a
n}中,即B⊆A.
∴对任意的n∈N
*,都有b
n∈A.
②∵数列{b
n}的第n项是数列{a
n}中第r项,
∴2×3
n-1=4r-2,
解得r=
,
∴T
n=3
n-1,(3分)
∴
=
=
.(2分)
点评:本题考查数列的通项公式的求法,考查关于数列的证明和极限的求法,解题时要认真审题,注意等价转化思想的合理运用.



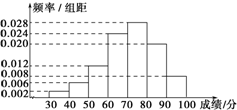 某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是
某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是