练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知a，b∈R，a2+b2=4，求3a+2b的取值范围为（ ）

    A.3a+2b≤4 B.3a+2b≤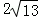 C.3a+2b≥4 D.不确定

     

    B

    【解析】

    试题分析：首先分析题目已知a2+b2=4，求3a+2b的取值范围．考虑到应用柯西不等式，首先构造出柯西不等式求出（3a+2b）2的最大值，开平方根即可得到答案．

    【解析】
    已知a2+b2=4和柯西不等式的二维形式（ac+bd）2≤（a2+b2）（c2+d2）

    故（3a+2b）2≤（a2+b2）（32+22）=52

    即：3a+2b≤

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 1.1整除练习卷（解析版） 题型：选择题

    存在整数n，使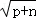+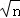是整数的质数p（ ）

    A.不存在

    B.只有一个

    C.多于一个，但为有限个

    D.有无穷多个

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.3排序不等式练习卷（解析版） 题型：解答题

    已知a，b，c为正数，用排序不等式证明：2（a3+b3+c3）≥a2（b+c）+b2（a+c）+c2（a+b）．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：填空题

    （2014•祁东县一模）已知a，b，c∈R，且2a+2b+c=8，则（a﹣1）2+（b+2）2+（c﹣3）2的最小值是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：选择题

    用柯西不等式求函数y=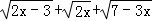的最大值为（ ）

    A.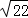 B.3 C.4 D.5

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明命题：“若a，b∈N，ab能被3整除，那么a，b中至少有一个能被3整除”时，假设应为（ ）

    A.a，b都能被3整除 B.a，b都不能被3整除

    C.a，b不都能被3整除 D.a不能被3整除

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明：将9个球分别染成红色或白色，那么无论怎么染，至少有5个球是同色的．其假设应是（ ）

    A.至少有5个球是同色的 B.至少有5个球不是同色的

    C.至多有4个球是同色的 D.至少有4个球不是同色的

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷（解析版） 题型：选择题

    求证：+＞．

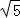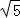    证明：因为+和都是正数，

    所以为了证明+＞，

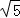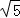    只需证明（+）2＞（）2，

    展开得5+2＞5，即2＞0，显然成立，

    所以不等式+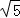＞．上述证明过程应用了（ ）

    A.综合法

    B.分析法

    C.综合法、分析法混合

    D.间接证法

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷（解析版） 题型：选择题

    （2013•滨州一模）已知不等式|x+2|+|x|≤a的解集不是空集，则实数a的取值范围是（ ）

    A.a＜2 B.a≤2 C.a＞2 D.a≥2

     

    查看答案和解析>>

    同步练习册答案