
| A. | $-\frac{11}{13}$ | B. | $-\frac{11}{12}$ | C. | $-\frac{7}{12}$ | D. | $-\frac{1}{13}$ |
分析 根据P为双曲线上的一点,若PF1与双曲线的一条渐近线平行,求出直线直线PF1的方程为y=$\frac{\sqrt{3}}{3}$(x+2),再联立双曲线$\frac{{x}^{2}}{3}$-y2=1的方程,求出点P的坐标,根据余弦定理即可求出答案.
解答 解:双曲线$\frac{{x}^{2}}{3}$-y2=1的两焦点分别为F1,F2,
∴a=$\sqrt{3}$,b=1,c=2,
渐近线方程为y=±$\frac{\sqrt{3}}{3}$x,
∴F1(-2,0),F2(2,0)
∵P为双曲线上的一点,PF1与双曲线的一条渐近线平行,
∴直线PF1的方程为y=$\frac{\sqrt{3}}{3}$(x+2),
由$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}(x+2)}\\{\frac{{x}^{2}}{3}-{y}^{2}=1}\end{array}\right.$,
解得x=-$\frac{7}{4}$,y=$\frac{\sqrt{3}}{12}$,
∴P(-$\frac{7}{4}$,$\frac{\sqrt{3}}{12}$),
∴|PF1|=$\frac{\sqrt{3}}{6}$,
∴|PF2|=2a+|PF1|=2$\sqrt{3}$+$\frac{\sqrt{3}}{6}$=$\frac{13\sqrt{3}}{6}$,
由cos∠F1PF2=$\frac{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-|{F}_{1}{F}_{2}{|}^{2}}{2•|P{F}_{1}|•|P{F}_{2}|}$=-$\frac{11}{13}$,
故选:A
点评 本题考查了双曲线的简单性质和余弦定理,属于中档题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | $y=±\sqrt{3}x$ | C. | y=±2x | D. | y=±3x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
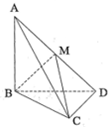 如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.
如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
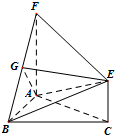 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com