
分析 由∠BAC是钝角可得$\overrightarrow{AB}•\overrightarrow{AC}<0$,由已知中两个向量的坐标,代入向量数量积公式,构造不等式,分析向量反向时的情况不存在可得答案.
解答 解:∵$\overrightarrow{AB}=(x,2x),\overrightarrow{AC}$=(3x,2),且∠BAC是钝角,
∴3x2+4x<0,解得$-\frac{4}{3}<x<0$,
由$\overrightarrow{AB}=λ\overrightarrow{AC}$,得(x,2x)=λ(3x,2),
即$\left\{\begin{array}{l}{x=3λx}\\{2x=2λ}\end{array}\right.$,解得λ=0或$λ=\frac{1}{3}$,
说明两向量不存在共线反向的情况.
故x的取值范围是($-\frac{4}{3},0$).
故答案为:($-\frac{4}{3},0$).
点评 本题考查的知识点是数量积表示两个向量的夹角,其中要注意分析两向量共线反向的情况,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
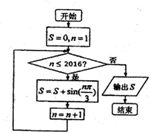
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 0 | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com