
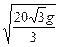 千米/秒,其中g为重力加速度,若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
千米/秒,其中g为重力加速度,若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少? 由题意可知,A、B、C舰的坐标为(3,0)、(-3,0)、(-5,2
由题意可知,A、B、C舰的坐标为(3,0)、(-3,0)、(-5,2 ).
). x-3y+7
x-3y+7 =0.
=0.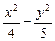 =1的右支上.
=1的右支上. ),此即为动物P的位置,利用两点间距离公式,可得|PA|=10
),此即为动物P的位置,利用两点间距离公式,可得|PA|=10
 ,所以直线PA的倾斜角为60°,于是舰A发射炮弹的方位角应是北偏东30°.
,所以直线PA的倾斜角为60°,于是舰A发射炮弹的方位角应是北偏东30°.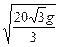 ,则
,则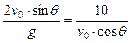 ,
,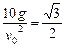 ,∴仰角θ=30°.
,∴仰角θ=30°.

科目:高中数学 来源:不详 题型:填空题
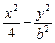 =1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.
=1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
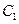 的渐近线方程是
的渐近线方程是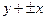 ,且它的一条准线与渐近线
,且它的一条准线与渐近线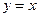 及
及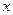 轴
轴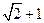
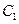 的两个顶点为焦点,以
的两个顶点为焦点,以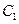 的焦点为顶点的椭圆
的焦点为顶点的椭圆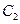 的方程;
的方程;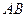 是椭圆
是椭圆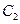 的长为
的长为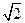 的动弦,
的动弦,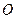 为坐标原来点,求
为坐标原来点,求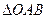 的面积
的面积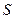 的取值范围。
的取值范围。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com