
| 学生编号 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 |
| 三项成绩 | 2,1,2 | 1,2,2 | 2,3,2 | 3,1,1 | 3,2,2 | 2,3,1 | 3,3,3 | 1,1,1 | 3,3,1 | 2,2,2 |
分析 根据题意得出表格的总分,(1)判断优秀的学生有:a3,a5,a7,运用古典概率求解即可,
(2)运用表格的数据得出总分小于6的有a1,a2,a4,a8,总分相同的有a1,a2,a4有3人,运用列举法得出事件判断个数即可.
解答 解:
| 学生编号 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 |
| 三项成绩 | 2,1,2 | 1,2,2 | 2,3,2 | 3,1,1 | 3,2,2 | 2,3,1 | 3,3,3 | 1,1,1 | 3,3,1 | 2,2,2 |
| 总分 | 5 | 5 | 7 | 5 | 7 | 6 | 9 | 3 | 7 | 6 |
点评 本题仔细阅读题意,考查了古典概率的求解,解决实际问题的能力,关键是列举事件判断即可.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB为圆O的直径,PB,PC分别与圆O相切于B,C两点,延长BA,PC相交于点D.
如图,AB为圆O的直径,PB,PC分别与圆O相切于B,C两点,延长BA,PC相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
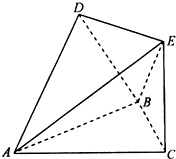 如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.
如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com