Question

4．已知函数$f（x）=\frac{ax}{{{x^2}+1}}（x∈R）$，如图是函数f（x）在[0，+∞）上的图象．
（1）求a的值，并判断函数的奇偶性补充作出函数f（x）在（-∞，0）上的图象，说明作图的理由；
（2）根据图象指出（不必证明）函数的单调区间与值域；

Answer 1

分析 （1）由f（1）=$\frac{a}{2}$=2，求得 a的值，可得f（x）的解析式．
（2）结合f（x）的图象可得函数的单调区间以及值域．

解答 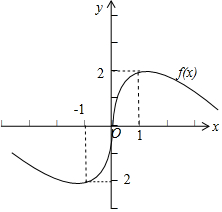解：（1）由函数$f（x）=\frac{ax}{{{x^2}+1}}（x∈R）$在[0，+∞）上的图象，可得f（1）=$\frac{a}{2}$=2，∴a=4，f（x）=$\frac{4x}{{x}^{2}+1}$．
由函数的解析式可得f（x）为奇函数，它的图象关于原点对称，
由此可得它在R上的图象．
（2）结合f（x）的图象可得函数的增区间为（-1，1），减区间为（-∞，-1）、（1，+∞）．
函数的值域为[-2，2]．

点评 本题主要考查奇函数的解析式，函数的奇偶性和单调性的应用，函数的值域，属于中档题．