
分析 (1)如图①,以V水、V人为邻边作?平行四边形,则此人的实际速度为V实=V水+V人,可得结论;
(2)如图②,解直角三角形可得|v实|=$\sqrt{{(4\sqrt{3})}^{2}-{4}^{2}}=4\sqrt{2}$(km/h),则tanθ=$\frac{|{v}_{人}|}{|{v}_{实}|}$=$\frac{4}{4\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
解答 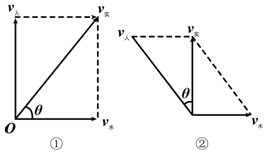 解:(1)如图①,由于V实=V水+V人,
解:(1)如图①,由于V实=V水+V人,
∴|V实|=$\sqrt{{(4\sqrt{3})}^{2}+{4}^{2}}=8$(km/h),
又tanθ=$\frac{|{v}_{人}|}{|{v}_{水}|}$=$\frac{4\sqrt{3}}{4}$=$\sqrt{3}$,
∴θ=60°,
∴他必须沿与河岸成60°角的方向前进,实际前进速度的大小为8km/h.
(2)如图②,解直角三角形可得|v实|=$\sqrt{{(4\sqrt{3})}^{2}-{4}^{2}}=4\sqrt{2}$(km/h),
又tanθ=$\frac{|{v}_{人}|}{|{v}_{实}|}$=$\frac{4}{4\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴他必须沿与水流方向成90°+θ(锐角θ满足$tanθ=\frac{\sqrt{2}}{2}$,或$sinθ=\frac{\sqrt{3}}{3}$等)方向航行,实际前进速度的大小为$4\sqrt{2}$(km/h).
点评 本题主要考查了向量在物理中的应用,解题时注意船在静水中速度,水流速度和船的实际速度三个概念的区分.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$或$\sqrt{5}$ | C. | $\sqrt{5}$或$2\sqrt{5}$ | D. | 以上都不是 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
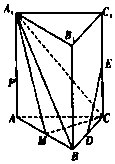 如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.
如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com