
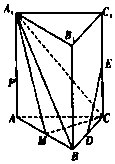
 如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.
如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.分析 (1)连接AC1,设O为A1C,AC1的交点,连接OM,OE,MD,推导出四边形MDEO为平行四边形,从而DE∥MO.由此能证明DE∥平面A1MC.
(2)以D为原点,DA为x轴,DB为y轴,过D作平面ABC的垂线为z轴,建系,利用向量法能求出存在点P,使得二面角A1-BC-P的余弦值为$\frac{{7\sqrt{19}}}{38}$,此时PA=1.
解答 证明:(1)如图,连接AC1,设O为A1C,AC1的交点,
由题意可知O为AC1的中点,连接OM,OE,MD,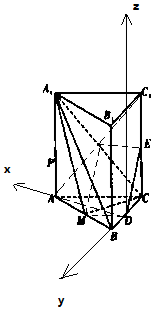
∵MD,OE分别为△ABC,△ACC1中的AC边上的中位线,
∴$\overrightarrow{MD}=\frac{1}{2}\overrightarrow{AC}$,$\overrightarrow{OE}=\frac{1}{2}\overrightarrow{AC}$,∴$\overrightarrow{MD}=\overrightarrow{OE}$,
∴四边形MDEO为平行四边形,∴DE∥MO.
又∵DE?平面A1MC,MO?平面A1MC,
∴DE∥平面A1MC.
解:(2)以D为原点,DA为x轴,DB为y轴,过D作平面ABC的垂线为z轴,建系,
设PA=a,则D(0,0,0),$A({\sqrt{3},0,0})$,$P({\sqrt{3},0,a})$,${A_1}({\sqrt{3},0,4})$,B(0,1,0),
则$\overrightarrow{PD}=({\sqrt{3},0,a})$,$\overrightarrow{PB}=({-\sqrt{3},1,-a})$,
设平面PBC的法向量为$\overrightarrow{n_1}=({{x_1},{y_1},{z_1}})$,
则$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{PD}=0\\ \overrightarrow{n_1}•\overrightarrow{PB}=0\end{array}\right.$解得$\overrightarrow{n_1}=({a,0,-\sqrt{3}})$.
同理,$\overrightarrow{{A_1}D}=({-\sqrt{3},0,-4})$,$\overrightarrow{{A_1}B}=({-\sqrt{3},1,-4})$,
设平面BCA1的法向量为$\overrightarrow{n_1}=({{x_2},{y_2},{z_2}})$,
则$\left\{\begin{array}{l}\overrightarrow{n_2}•\overrightarrow{{A_1}D}=0\\ \overrightarrow{n_2}•\overrightarrow{{A_1}B}=0\end{array}\right.$解得$\overrightarrow{n_2}=({4,0,-\sqrt{3}})$.
如图易得所求二面角为锐角,设为θ,
则$cosθ=|{\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|{\overrightarrow{n_1}}||{\overrightarrow{n_2}}|}}}|=|{\frac{4a+3}{{\sqrt{{a^2}+3}•\sqrt{19}}}}|=\frac{{7\sqrt{19}}}{38}$,
解得a=1或$-\frac{37}{5}$(舍),
所以存在点P,使得二面角A1-BC-P的余弦值为$\frac{{7\sqrt{19}}}{38}$,此时PA=1.
点评 本题考查线面平行的证明,考查考查满足条件的点的位置的判断与求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | g(x)在区间[-$\frac{π}{12},\frac{π}{3}$]上的最小值为-1. | |
| B. | g(x)的图象可由函数f(x)向上平移2个单位,在向右平移$\frac{π}{3}$个单位得到. | |
| C. | g(x)的图象可由函数f(x)的图象先向左平移$\frac{π}{3}$个单位得到. | |
| D. | g(x)的图象可由函数f(x)的图象先向右平移$\frac{π}{3}$个单位得到. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{3},1})$ | B. | $({-∞,\frac{1}{3}})∪({1,+∞})$ | C. | $({-\frac{1}{3},\frac{1}{3}})$ | D. | $({-∞,-\frac{1}{3}})∪({\frac{1}{3},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | 3 | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com