
在平面直角坐标系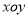 中,点
中,点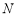 与点
与点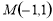 关于原点
关于原点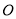 对称,
对称,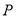 是动点,且直线
是动点,且直线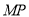 与
与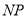
的斜率之积等于 .
.
(Ⅰ)求动点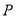 的轨迹方程;
的轨迹方程;
(Ⅱ)设直线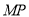 和
和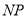 与直线
与直线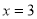 分别交于
分别交于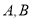 两点,问:是否存在点
两点,问:是否存在点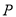 使得
使得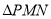 与
与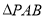 的面
的面
积相等?若存在,求出点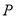 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

科目:高中数学 来源:2015-2016学年海南省高一上学期期中数学试卷(解析版) 题型:解答题
为了预防甲型H1N1流感,某学校对教室用药薰消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与t时间(小时)成正比,药物释放完毕后,y与t之间的函数关系式为 (a为常数)如下图所示,根据图中提供的信息,回答下列问题.
(a为常数)如下图所示,根据图中提供的信息,回答下列问题.

(1)从药物释放开始,求每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始至少需要经过多少小时后,学生才可能回到教室.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省高一下学期期中数学试卷(解析版) 题型:解答题
设各项均为正数的数列 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 恰好是等比数列
恰好是等比数列 的前三项.
的前三项.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)记数列 的前
的前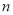 项和为
项和为 ,若对任意的
,若对任意的 ,
,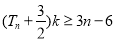 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年山西省临汾市高一12月月考数学试卷(解析版) 题型:解答题
已知函数 有如下性质:如果常数
有如下性质:如果常数 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.
(1)已知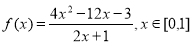 ,利用上述性质,求函数
,利用上述性质,求函数 的单调区间和值域;
的单调区间和值域;
(2)对于(1)中的函数 和函数
和函数 ,若对任意
,若对任意 ∈[0,1],总存在
∈[0,1],总存在 ∈[0,1],使得
∈[0,1],使得 =
= 成立,求实数
成立,求实数 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2016届宁夏银川一中高三上学期第四次月考理科数学试卷(解析版) 题型:解答题
已知函数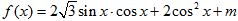 在区间
在区间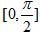 上的最大值为2.
上的最大值为2.
(1)求常数m的值;
(2)在△ABC中,角A、B、C所对的边是a、b、c,若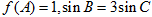 ,△ABC面积为
,△ABC面积为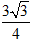 .求边长a.
.求边长a.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁省高二12月月考理科数学卷(解析版) 题型:解答题
已知椭圆 的离心率为
的离心率为 ,短轴端点到焦点的距离为2.
,短轴端点到焦点的距离为2.
(1)求椭圆 的方程;
的方程;
(2)设点 是椭圆
是椭圆 上的任意两点,
上的任意两点,  是坐标原点,且
是坐标原点,且 .
.
①求证:原点 到直线
到直线 的距离为定值,并求出该定值;
的距离为定值,并求出该定值;
②任取以椭圆 的长轴为直径的圆上一点
的长轴为直径的圆上一点 ,求
,求 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省高二上期中文科数学试卷(解析版) 题型:解答题
已知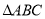 的三个顶点的坐标为
的三个顶点的坐标为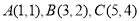 .
.
(1)求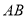 边上的高所在直线的方程;
边上的高所在直线的方程;
(2)若直线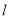 与
与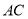 平行,且在
平行,且在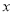 轴上的截距比在
轴上的截距比在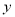 轴上的截距大1,求直线
轴上的截距大1,求直线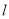 与两条坐标轴围成的三角形的周长.
与两条坐标轴围成的三角形的周长.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年宁夏石嘴山三中高二上期中理科数学试卷(解析版) 题型:填空题
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据,求得线性回归方程为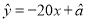 .若在这些样本点中任取一点,则它在回归直线左下方
.若在这些样本点中任取一点,则它在回归直线左下方
的概率为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com