
分析 (1)首先对f(x)求导f'(x)=3x2-4x+1=(x-1)(3x-1),判断导函数的零点;
(2)利用导函数图形来判断原函数f(x)的图象,求出最值;
解答 解:(Ⅰ)因为f(x)=x3-2x2+x,
∴f'(x)=3x2-4x+1=(x-1)(3x-1),
令f'(x)>0得:x>1或x<$\frac{1}{3}$;
f'(x)<0得:$\frac{1}{3}<\\;x\\;<1$ x<1,
∴函数f(x)的单调递增区间为:(-∞,$\frac{1}{3}$),(1,+∞)
函数f(x)的单调递减区间为($\frac{1}{3}$,1)
(Ⅱ)由(Ⅰ)知:f(x),f'(x) 的变化情况如下表:
| x | (-∞,$\frac{1}{3}$) | $\frac{1}{3}$ | ($\frac{1}{3}$,1) | 1 | (1,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值$\frac{4}{27}$ | 单调递减 | 极小值0 | 单调递增 |
点评 本题主要考查了利用导数求函数的单调区间,以及函数的最值问题,属基础题;


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 20 | C. | 16 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,D是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
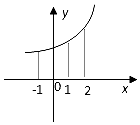 已知函数y=f(x)的图象如图所示,设函数y=f(x)从-1到1的平均变化率为v1,从1到2的平均变化率为v2,则v1与v2的大小关系为( )
已知函数y=f(x)的图象如图所示,设函数y=f(x)从-1到1的平均变化率为v1,从1到2的平均变化率为v2,则v1与v2的大小关系为( )| A. | v1>v2 | B. | v1=v2 | C. | v1<v2 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com