
| A. | (2,1) | B. | (-2,-1) | C. | (2,1)或(-2,-1) | D. | (2,-1)或(-2,1) |
分析 可设$\overrightarrow{b}=(x,y)$,根据条件便可以得到$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=5}\\{x-2y=0}\end{array}\right.$,这样解方程组便可得出x,y的值,从而求出$\overrightarrow{b}$的坐标.
解答 解:设$\overrightarrow{b}=(x,y)$,由$|\overrightarrow{b}|=\sqrt{5}$得,$\sqrt{{x}^{2}+{y}^{2}}=\sqrt{5}$;
∴x2+y2=5①;
又$\overrightarrow{a}=(2,-4)$与$\overrightarrow{b}$垂直;
∴(2,-4)•(x,y)=2x-4y=0;
即x=2y,带入①可得y=±1;
∴$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.,或\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$;
∴$\overrightarrow{b}=(2,1)$,或(-2,-1).
故选:C.
点评 考查根据向量的坐标求向量的长度,向量垂直的充要条件,以及向量数量积的坐标运算.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}+\frac{π}{8}$ | B. | $\frac{1}{3}+\frac{π}{4}$ | C. | $\frac{1}{6}+\frac{π}{4}$ | D. | $\frac{1}{3}+\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
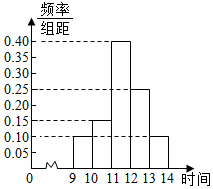 某商场在庆元宵节促销活动中,对元宵节9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售额为10万元.
某商场在庆元宵节促销活动中,对元宵节9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售额为10万元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com