
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) | ||
| B、(2,1) | ||
C、(1,
| ||
D、(
|
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
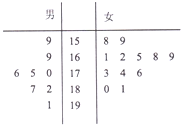 第117届中国进出口商品交易会(简称2015年春季交广会)将于2015年4月15日在广州市举行,为了搞好接待工作,组委会在广州某大学分别招募8名男志愿者和12名女志愿者,现将这20名志愿者的身高组成如下茎叶图(单位:m),若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.
第117届中国进出口商品交易会(简称2015年春季交广会)将于2015年4月15日在广州市举行,为了搞好接待工作,组委会在广州某大学分别招募8名男志愿者和12名女志愿者,现将这20名志愿者的身高组成如下茎叶图(单位:m),若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.查看答案和解析>>
科目:高中数学 来源: 题型:
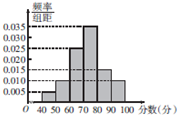 某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )
某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )| A、120 | B、150 |
| C、180 | D、200 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a+1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OQ |
| PF1 |
| PF2 |
| OT |
| MN |
| OM |
| ON |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com