
| 1 |
| an-2 |
| 1 | ||
|
| 7 |
| 30 |
| 1 |
| 4 |
| 1 |
| an-2 |
| 1 | ||
|
| 1 |
| an-2 |
| 1 |
| an+1-2 |
2 n |
| 1 |
| an-2 |
| 1 | ||
|
| 1 |
| an-2 |
| 1 |
| an+1-2 |
| 1 |
| a1-2 |
| 1 |
| a2-2 |
| 1 |
| a2-2 |
| 1 |
| a3-2 |
| 1 |
| an-2 |
| 1 |
| an+1-2 |
| 1 |
| a1-2 |
| 1 |
| an+1-2 |
| 1 |
| 4 |
| 1 |
| 23•2n-4 |
| 7 |
| 30 |
| 1 |
| 4 |


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
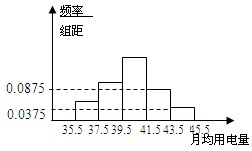 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下;其中直方图从左到右前3个小矩形的面积之比为1:2:3.
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下;其中直方图从左到右前3个小矩形的面积之比为1:2:3.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.查看答案和解析>>
科目:高中数学 来源: 题型:
|
| AC |
| AB |
| AC |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,
如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,| CM |
| MP |
| BN |
| NA |
查看答案和解析>>
科目:高中数学 来源: 题型:
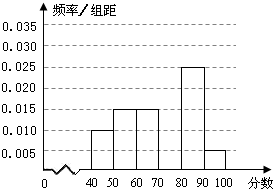 某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:
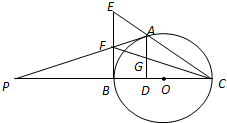 如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com