
分析 (1)根据函数奇偶性的定义求出a的值即可;(2)根据复合函数“同增异减”的性质判断函数的单调性即可;(3)构造新函数求出新函数的单调性,得到函数的最小值,从而求出m的范围即可.
解答 (1)∵f(x)是奇函数,∴定义域关于原点对称,
由 $\frac{1-ax}{x-1}$>0,得(x-1)(1-ax)>0,
令(x-1)(1-ax)=0,得x1=1,x2=$\frac{1}{a}$,
∴$\frac{1}{a}$=-1,解得a=-1.
(2)令u(x)=$\frac{1+x}{x-1}$=1+$\frac{2}{x-1}$,
设任意x1<x2,且x1,x2∈(1,+∞),
则u(x1)-u(x2)=$\frac{2{(x}_{2}{-x}_{1})}{{(x}_{1}-1){(x}_{2}-1)}$,
∵1<x1<x2,∴x1-1>0,x2-1>0,x2-x1>0,
∴u(x1)-u(x2)>0,即u(x1)>u(x2).
∴u(x)=1+$\frac{2}{x-1}$(x>1)是减函数,
又y=${log}_{\frac{1}{2}}$u为减函数,
∴f(x)=${log}_{\frac{1}{2}}^{\frac{x+1}{x-1}}$在(1,+∞)上为增函数.
(3)由题意知${log}_{\frac{1}{2}}^{\frac{x+t+1}{x+t-1}}$-($\frac{1}{2}$)x>m,x∈[3,4]时恒成立,
令g(x)=${log}_{\frac{1}{2}}^{\frac{x+t+1}{x+t-1}}$-($\frac{1}{2}$)x>log,x∈[3,4],
由(1)知${log}_{\frac{1}{2}}$$\frac{x+t+1}{x+t-1}$在[3,4]上为增函数,
又-($\frac{1}{2}$)x在[3,4]上也是增函数,
故g(x)在[3,4]上为增函数,
∴g(x)的最小值为g(3)=${log}_{\frac{1}{2}}^{\frac{t+4}{t+2}}$-($\frac{1}{2}$)3>${log}_{\frac{1}{2}}^{2}$-$\frac{1}{8}$=-$\frac{9}{8}$,
∴m≤-$\frac{9}{8}$,故实数m的范围是(-∞,-$\frac{9}{8}$].
点评 本题考查了函数的奇偶性问题,考查函数的单调性、最值问题,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}π$ | B. | $\frac{π}{2}$ | C. | $\frac{\sqrt{3}}{2}π$ | D. | $\frac{\sqrt{3}}{4}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
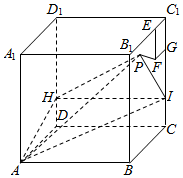 如图所示,正方体ABCD-A1B1C1D1棱长为4,点H在棱DD1上,点I在棱CC1上,且HD=CI=1,在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1,侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍,则当点P运动时,三棱锥A-HPI的体积的最小值是( )
如图所示,正方体ABCD-A1B1C1D1棱长为4,点H在棱DD1上,点I在棱CC1上,且HD=CI=1,在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1,侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍,则当点P运动时,三棱锥A-HPI的体积的最小值是( )| A. | $\frac{2\sqrt{17}}{3}$ | B. | $\frac{25}{6}$ | C. | $\frac{2\sqrt{17}}{3}$(10-3$\sqrt{2}$) | D. | $\frac{20}{3}$-2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{6}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com