
已知定义在区间(0,+∞)上的函数f(x)满足f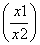 =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,求f(x)在[2,9]上的最小值.
科目:高中数学 来源: 题型:
下列命题中是真命题的为( )
A.命题“若x2-3x+2=0,则x=1”的否命题是“若x2-3x+2=0,则x≠1”
B.命题p:∃x0∈R,sin x0>1,则綈p:∀x∈R,sin x≤1
C.若p且q为假命题,则p,q均为假命题
D.“φ=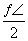 +2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件
+2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
如图1是某公共汽车线路收支差额y元与乘客量x的图像.

(1)试说明图1上点A、点B以及射线AB上的点的实际意义;
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的建议,如图2、3所示.你能根据图像,说明这两种建议的意义吗?
(3)此问题中直线斜率的实际意义是什么?
(4)图1、图2、图3中的票价分别是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
已知奇函数f(x)对任意的正实数x1,x2(x1≠x2),恒有(x1-x2)(f(x1)-f(x2))>0,则一定正确的是( )
A.f(4)>f(-6) B.f(-4)<f(-6)
C.f(-4)>f(-6) D.f(4)<f(-6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com