

分析 (1)当点A在平面BCDM上的投影在MB上时,求直线AC与平面BCDM所成角的正弦值;
(2)当点A在平面BCDM上的投影在DC上时,求平面ABC与平面AMD所成二面角的正切值.
解答  解:(1)当点A在平面BCDM上的投影在MB上时,
解:(1)当点A在平面BCDM上的投影在MB上时,
即AH⊥面BCDM,
则AH⊥MB,
则∠ACH是直线AC与平面BCDM所成的角,
则矩形中,过H分别作HF⊥AB,HG⊥BG,
∵AD=4,AB=6,且MD=1,
∴AM=3,BM=$\sqrt{A{M}^{2}+A{B}^{2}}$=3$\sqrt{5}$,
则AH=$\frac{AM•AB}{MB}$=$\frac{3×6}{3\sqrt{5}}$=$\frac{6}{\sqrt{5}}$,
AH2=AF•AB,
即AF=$\frac{A{H}^{2}}{AB}$=$\frac{\frac{36}{5}}{6}$=$\frac{6}{5}$,HF=$\sqrt{A{H}^{2}-A{F}^{2}}$=$\frac{12}{5}$,
则CG=CB-BG=6-$\frac{12}{5}$=$\frac{18}{5}$,HG=BF=AB-AF=6-$\frac{6}{5}$=$\frac{24}{5}$,
则CH=$\sqrt{C{G}^{2}+G{H}^{2}}$=6,
AC=$\sqrt{C{H}^{2}+A{H}^{2}}$=$\sqrt{36+\frac{36}{5}}$=$\frac{6\sqrt{30}}{5}$,
则sin∠ACH=$\frac{AH}{AC}$=$\frac{\frac{6}{\sqrt{5}}}{\frac{6\sqrt{30}}{5}}$=$\frac{\sqrt{6}}{6}$,
即直线AC与平面BCDM所成角的正弦值为$\frac{\sqrt{6}}{6}$;
(2)当点A在平面BCDM上的投影在DC上时,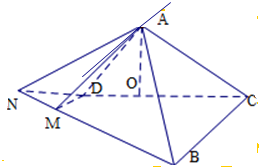
∵MD∥BC,
∴过A点作BC的平行线,
∵点A在平面BCDM上的投影在DC上,BC⊥CD,
∴BC⊥面ACD,
∴BC⊥AD,BC⊥AC,
∴可以得到∠DAC即为所求的二面角.
∵MD=1,∴AM=3,
折叠后AD=$\sqrt{A{M}^{2}-D{M}^{2}}$=$\sqrt{9-1}=\sqrt{8}$=2$\sqrt{2}$,
在直角三角形ACB中,BC=4,AB=6,
则AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{36-16}=\sqrt{20}$=2$\sqrt{5}$,
由余弦定理得cos∠DAC=$\frac{A{D}^{2}+A{C}^{2}-C{D}^{2}}{2AD•AC}$=$\frac{8+20-36}{2×2\sqrt{2}×2\sqrt{5}}$=$-\frac{1}{\sqrt{10}}$,
sin∠DAC=$\frac{3}{\sqrt{10}}$,
则平面ABC与平面AMD所成二面角的正切值tan∠DAC=$\frac{-\frac{1}{\sqrt{10}}}{\frac{3}{\sqrt{10}}}$=-$\frac{1}{3}$.
点评 本题主要考查空间直线和平面所成的角以及二面角的应用,综合性较强,运算量较大,有一定的难度.


科目:高中数学 来源: 题型:解答题
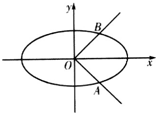 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{6}}}{3}$,点O为坐标原点,椭圆C与曲线|y|=x的交点分别为A,B(A在第四象限),且$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{6}}}{3}$,点O为坐标原点,椭圆C与曲线|y|=x的交点分别为A,B(A在第四象限),且$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 11 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{5}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com