考点:两角和与差的正弦函数,平面向量数量积的运算,正弦函数的单调性
专题:三角函数的求值,三角函数的图像与性质
分析:(1)由已知中已知
=(5
cosx,cosx),
=(sinx,2cosx),函数f(x)=
•
+|
|
2,结合降次升角公式及和差角公式,将函数解析式化为正弦型函数,进而由正弦型函数的图象和性质,求出函数y=f(x)的周期和对称轴方程;
(2)由(1)中函数解析式及
2kπ+≤2x+≤2kπ+,求出自变量x的取值范围,可得函数y=f(x)的单调递减区间.
解答:
解:(1)∵
=(5
cosx,cosx),
=(sinx,2cosx),
∴
•=5cosxsinx+2cos2x,||2=sin2x+4cos2x…(2分)
∴
f(x)=5cosxsinx+2cos2x+sin2x+4cos2x=5cosxsinx+6cos2x+sin2x…(3分)
=
sin2x+5+1=sin2x++…(5分)
=
5(sin2x•+cos2x•)+=5sin(2x+)+…(6分)
∵ω=2,
∴
T==π; …(7分)
由
2x+=kπ+,
得
x=+,k∈Z为对称轴方程; …(9分)
(2)由
2kπ+≤2x+≤2kπ+,得:
kπ+≤x≤kπ+,k∈Z…(12分)
所以函数的单调递减区间为
[kπ+,kπ+],k∈Z…(13分)
点评:本题考查的知识点是两角差的正弦函数公式,三角函数的周期性,对称性及单调区间,是三角函数图象和性质的综合应用,难度中档.



 科学实验活动册系列答案
科学实验活动册系列答案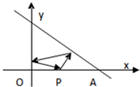 如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射到P点.求(1)光线所经过的路程是多少;(2)直线AB关于直线2x-y-2=0的对称直线.
如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射到P点.求(1)光线所经过的路程是多少;(2)直线AB关于直线2x-y-2=0的对称直线.