
分析 (1)当x=$\frac{π}{4}$时,利用cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|a|•|b|}$,即可求向量向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ;
(2)化简 $\overrightarrow{c}•\overrightarrow{d}$的表达式,通过相位的范围,利用正弦函数的值域求解其最大值;
(3)通过三角变换求出函数g(x)的表达式,与g(x)=2sin2x+1对照比较,得到$\overrightarrow{m}$=(s,t),即可求|$\overrightarrow{m}$|的最小值.
解答 解:(1)当x=$\frac{π}{4}$时,向量$\overrightarrow{a}$=($\sqrt{3}$cosx,cosx)=($\frac{\sqrt{6}}{2}$,$\frac{\sqrt{2}}{2}$ ),$\overrightarrow{b}$=(0,sinx)=(0,$\frac{\sqrt{2}}{2}$),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=($\frac{\sqrt{6}}{2}$,$\frac{\sqrt{2}}{2}$ )•(0,$\frac{\sqrt{2}}{2}$)=$\frac{1}{2}$,
而|$\overrightarrow{a}$|=$\sqrt{(\frac{\sqrt{6}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}$=$\sqrt{2}$,|$\overrightarrow{b}$|=$\sqrt{0+(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{2}}{2}$,
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|a|•|b|}$=$\frac{\frac{1}{2}}{\sqrt{2}×\frac{\sqrt{2}}{2}}$=$\frac{1}{2}$,即θ=$\frac{π}{3}$;
(2)$\overrightarrow{c}•\overrightarrow{d}$=(sinx,cosx)•(sinx,sinx)
=sin2x+sinxcosx
=$\frac{1-cos2x}{2}$+$\frac{1}{2}$sin2x
=$\frac{1}{2}$+$\frac{1}{2}$(sin2x-cos2x)
=$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$).
∴当2x-$\frac{π}{4}$=$\frac{π}{2}$+2kπ即x=$\frac{3π}{8}$+kπ,(k∈Z)时,$\overrightarrow{c}•\overrightarrow{d}$取得最大值$\frac{\sqrt{2}+1}{2}$;
(3)f(x)=($\overrightarrow{a}-\overrightarrow{b}$)$•(\overrightarrow{c}+\overrightarrow{d})$
=($\sqrt{3}$cosx,cosx-sinx)•(2sinx,cosx+sinx)
=2$\sqrt{3}$sinxcosx+cos2x-sin2x
=$\sqrt{3}$sin2x+cos2x
=2sin(2x+$\frac{π}{6}$).
g(x)=f(x-s)+t=2sin[2(x-s)+$\frac{π}{6}$]+t=2sin(2x-2s+$\frac{π}{6}$)+t=2sin2x+1,
∴t=1,s=$\frac{π}{12}$+kπ,(k∈Z)
∴|$\overrightarrow{m}$|=$\sqrt{{s}^{2}+{t}^{2}}$=$\sqrt{(\frac{π}{12}+kπ)^{2}+1}$,
∴当k=0时,∴|$\overrightarrow{m}$|min=$\sqrt{(\frac{π}{12})^{2}+1}$=$\frac{\sqrt{{π}^{2}+144}}{12}$.
点评 本题考查向量的数量积,两角和与差的三角函数,三角函数图象的平移变换,向量的模等知识,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{8}{27}$ | D. | $\frac{19}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
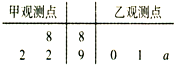 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3<b3 | B. | ab>b2 | C. | ac2>bc2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
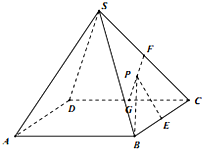 如图,正四棱锥S-ABCD中.SA=AB=2,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.
如图,正四棱锥S-ABCD中.SA=AB=2,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com