
已知函数f(x)=x2+ax-lnx,a∈R。
(1)若函数f(x)在上是减函数,求实数a的取值范围;
(2)令g(x)=f(x)-x2,是否存在实数a,当x∈(0,e](e是自然对数的底数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
解:(1)f′(x)=2x+a-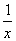 =
=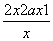 ≤0在上恒成立
≤0在上恒成立
令h(x)=2x2+ax-1,x∈,∴h(x)≤0在上恒成立
∴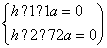 得
得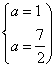 ,∴a≤-
,∴a≤-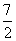 . --------5分
. --------5分
(2)假设存在实数a,使g(x)=f(x)-x2,x∈(0,e]有最小值3
g(x)=ax-lnx,x∈(0,e],g′(x)=a-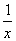 =
=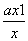
①当a≤0时,g′(x)<0,g(x)在(0,e]上单调递减
∴g(x)min=g(e)=ae-1=3,∴a=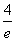 (舍去)
(舍去)
②当0<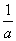 <e即a>
<e即a> 时,在(0,
时,在(0,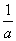 )上,g′(x)<0;在(
)上,g′(x)<0;在(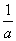 ,e]上,g′(x)>0
,e]上,g′(x)>0
∴g(x)在(0,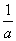 ]上单调递减,在(
]上单调递减,在(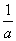 ,e]上单调递增
,e]上单调递增
∴g(x)min=g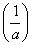 =1+lna=3,∴a=e2满足条件
=1+lna=3,∴a=e2满足条件
③当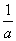 ≥e即0<a≤
≥e即0<a≤ 时,g′(x)<0,g(x)在(0,e]上单调递减
时,g′(x)<0,g(x)在(0,e]上单调递减
g(x)min=g(e)=ae-1=3
∴a=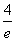 >
> (舍去)
(舍去)
综上所述:a=e2 --------10分


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
(1)证明B1C1⊥CE;
(2)求二面角B1-CE-C1的余弦值;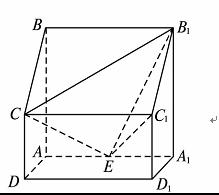
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为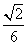 ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列六种图象变换方法:
①图象上所有点的横坐标缩短到原来的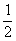 ,纵坐标不变;
,纵坐标不变;
②图象上所有点的横坐标伸长到原来的2倍,纵坐标不变;
③图象向右平移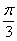 个单位;④图象向左平移
个单位;④图象向左平移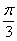 个单位;
个单位;
⑤图象向右平移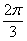 个单位;⑥图象向左平移
个单位;⑥图象向左平移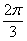 个单位.
个单位.
请用上述变换中的两种变换,将函数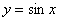 的图象变换到函数
的图象变换到函数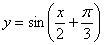 的图象,那么这两种变换的序号依次是_______
的图象,那么这两种变换的序号依次是_______
(填上一种你认为正确的答案即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com