
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
(1)证明B1C1⊥CE;
(2)求二面角B1-CE-C1的余弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为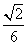 ,求线段AM的长.
,求线段AM的长.
(方法一)(1)证明:如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),B(0,0,2),C(1,0,1),B1(0,2,2),C1(1,2,1),E(0,1,0).
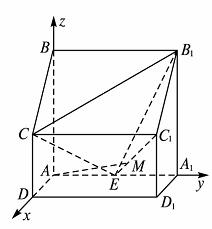
易得 =(1,0,-1),
=(1,0,-1),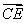 =(-1,1,-1),于是
=(-1,1,-1),于是 ·
·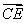 =0,
=0,
所以B1C1⊥CE.
(2)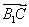 =(1,-2,-1).
=(1,-2,-1).
设平面B1CE的法向量m=(x,y,z),
则 即
即
消去x,得y+2z=0,不妨令z=1,可得一个法向量为m=(-3,-2,1).
由(1),B1C1⊥CE,又CC1⊥B1C1,可得B1C1⊥平面CEC1,
故 =(1,0,-1)为平面CEC1的一个法向量.
=(1,0,-1)为平面CEC1的一个法向量.
于是cos〈m, 〉=
〉= ,
,
因为二面角B1-CE-C1的平面角是锐角
所以二面角B1-CE-C1的余弦值为 .
.
(3) =(0,1,0),
=(0,1,0), =(1,1,1).
=(1,1,1).
设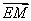 =λ
=λ =(λ,λ,λ),0≤λ≤1,有
=(λ,λ,λ),0≤λ≤1,有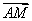 =
= +
+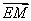 =(λ,λ+1,λ).
=(λ,λ+1,λ).
可取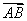 =(0,0,2)为平面ADD1A1的一个法向量.
=(0,0,2)为平面ADD1A1的一个法向量.
设θ为直线AM与平面ADD1A1所成的角,则
sin θ=|cos〈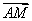 ,
,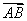 〉|=
〉|=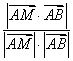
= .
.
于是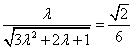 ,解得
,解得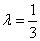 ,
,
所以AM=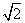 .
.
(方法二) (1)证明:因为侧棱CC1⊥底面A1B1C1D1,B1C1 平面A1B1C1D1,
平面A1B1C1D1,
 所以CC1⊥B1C1.
所以CC1⊥B1C1.
经计算可得B1E=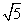 ,B1C1=
,B1C1=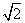 ,EC1=
,EC1=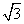 ,
,
从而B1E2= ,
,
所以在△B1EC1中,B1C1⊥C1E,
又CC1,C1E 平面CC1E,CC1∩C1E=C1,
平面CC1E,CC1∩C1E=C1,
所以B1C1⊥平面CC1E,
又CE 平面CC1E,故B1C1⊥CE.
平面CC1E,故B1C1⊥CE.
(2)过B1作B1G⊥CE于点G,连接C1G.
由(1),B1C1⊥CE,故CE⊥平面B1C1G,得CE⊥C1G,
所以∠B1GC1为二面角B1-CE-C1的平面角.
在△CC1E中,由CE=C1E=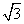 ,CC1=2,可得C1G=
,CC1=2,可得C1G= .
.
在Rt△B1C1G中,B1G= ,
,
所以二面角B1-CE-C1的余弦值为 .
.
(3)连接D1E,过点M作MH⊥ED1于点H,可得MH⊥平面ADD1A1,连接AH,AM,则∠MAH为直线AM与平面ADD1A1所成的角.
设AM=x,从而在Rt△AHM中,有MH=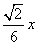 ,AH=
,AH= .
.
在Rt△C1D1E中,C1D1=1,ED1=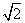 ,得EH=
,得EH= .
.
在△AEH中,∠AEH=135°,AE=1,
由AH2=AE2+EH2-2AE·EHcos 135°,得 ,
,
整理得5x2- -6=0,解得x=
-6=0,解得x=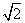 .
.
所以线段AM的长为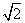 .
.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
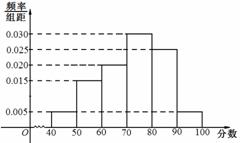
某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人。
(1)求N的值并估计这次测试数学成绩的平均分和众数;
(2)学校从成绩在[70,100]的三组学生中用分层抽样的方法抽取12名学生进行复试,若成绩在[80,90)这一小组中被抽中的学生实力相当,且能通过复试的概率均为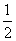 ,设成绩在[80,90)这一小组中被抽中的学生中能通过复试的人数为
,设成绩在[80,90)这一小组中被抽中的学生中能通过复试的人数为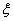 ,求
,求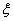 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于R上可导的任意函数f(x),且 若满足(x-1)
若满足(x-1) >0,则必有 ( )
>0,则必有 ( )
A、f(0)+f(2)2f(1) B、f(0)+f(2)2f(1)
C、f(0)+f(2)>2f(1) D、f(0)+f(2)2f(1)
查看答案和解析>>
科目:高中数学 来源: 题型:
箱中装有标号为1,2,3,4,5,6且大小相同的6个球.从箱中一次摸出两个球,记下号码并放回,如果两球号码之积是4的倍数,则获奖.现有4人参与摸奖(每人一次),则恰好有3人获奖的概率是( )
A.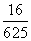 B.
B.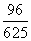 C.
C.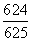 D.
D.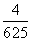
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x2+ax-lnx,a∈R。
(1)若函数f(x)在上是减函数,求实数a的取值范围;
(2)令g(x)=f(x)-x2,是否存在实数a,当x∈(0,e](e是自然对数的底数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com