Question

根据要求证明下列各题：
（1）用分析法证明：
（2）用反证法证明：1，，3不可能是一个等差数列中的三项

Answer 1

（1）详见解析，（2）详见解析.

解析试题分析：（1）分析法证明，从所求证结论出发，找出其成立的必要条件，直至这个条件为已知条件或恒成立条件. 要证：；即证：即证：即证：即证：；即证：；而显然成立，且以上各步皆可逆,所以：,（2）反证法用于直接证明结论比较困难或繁琐，而其反面较简单的情况.注意反设是要全面、正确. 假设1，，3是某一个等差数列中的三项，且分别是第项（），
则数列的公差，则，因为，所以，所以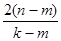为有理数，所以是有理数，这与是无理数相矛盾. 故假设不成立，所以1，，3不可能是某等差数列的三项.
试题解析：（1）要证：；即证：；
即证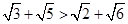：；即证：；
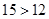即证：；即证：；而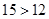显然成立，且以上各步皆可逆，
所以：        7分
（其他方法参照给分）
（2）假设1，，3是某一个等差数列中的三项，且分别是第项（），    9分
则数列的公差，则，
因为，所以，所以为有理数，    12分
所以是有理数，这与是无理数相矛盾。
故假设不成立，所以1，，3不可能是某等差数列的三项。    14分
考点：分析法及反证法