练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

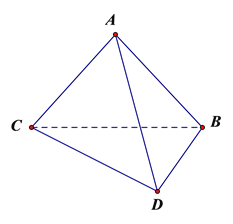
    【题目】如图，将一副三角板拼接，使他们有公共边BC，且使这两个三角形所在的平面互相垂直，，，，BC=6.

    （1）证明：平面ADC平面ADB；

    （2）求二面角A—CD—B平面角的正切值.

    【答案】（1）见解析（2）2

    【解析】试题分析：（1）先根据面面垂直性质定理得，即得.再根据以及线面垂直判定定理得.最后根据面面垂直判定定理得结论，（2）取BC的中点，根据等腰三角形性质得，再根据面面垂直性质定理得再作，则根据三垂线定理得，由二面角定义得是二面角的平面角.最后解直角三角形得二面角A—CD—B平面角的正切值.

    试题解析：（1）证明：因为，

    所以.

    又，所以.

    又，且，

    所以.

    又，所以.

    （2）取BC的中点，连接，则，

    又 所以

    所以过作，连接，则则所以是二面角的平面角.

    在中，，又，

    所以，即二面角平面角的正切值为2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，直三棱柱中， ， ， ，点， 分别是的中点.

    （Ⅰ）求证： 平面；

    （Ⅱ）若二面角的大小为，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若曲线在点处的切线与直线垂直，求函数的极值；

    （2）设函数.当=时，若区间[1，e]上存在x0，使得，求实数的取值范围．（为自然对数底数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(1)求函数的零点个数；

    (2)证明：当，函数有最小值，设的最小值为，求函数的值域.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知曲线的参数方程为（为参数）.以直角坐标系的原点为极点，轴的正半轴为极轴建立坐标系，曲线的极坐标方程为.

    （1）求的普通方程和的直角坐标方程；

    （2）若过点的直线与交于，两点，与交于，两点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数的定义域为，若满足条件：存在，使在上的值域为，则称为“倍缩函数”．若函数为“倍缩函数”，则实数的取值范围是

    A. （﹣∞，ln2﹣1） B. （﹣∞，ln2﹣1]

    C. （1﹣ln2，+∞） D. [1﹣ln2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且经过点.

    （1）求椭圆的标准方程；

    （2）过点的直线交椭圆于两点，是轴上的点，若是以为斜边的等腰直角三角形， 求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了检验学习情况，某培训机构于近期举办一场竞赛活动，分别从甲、乙两班各抽取10名学员的成绩进行统计分析，其成绩的茎叶图如图所示（单位：分），假设成绩不低于90分者命名为“优秀学员”.

    （1）分别求甲、乙两班学员成绩的平均分（结果保留一位小数）；

    （2）从甲班4名优秀学员中抽取两人，从乙班2名80分以下的学员中抽取一人，求三人平均分不低于90分的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列中，已知，．　

    （Ⅰ）设，求数列的通项公式；

    （Ⅱ）设，求数列的前项和.

    查看答案和解析>>

    同步练习册答案