
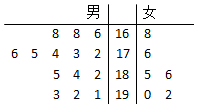
 M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.分析 (1)利用茎叶图能求出男生成绩的中位数及女生成绩的平均值.
(2)用分层抽样的方法从“甲部门”和“乙部门”20人中抽5人,选中的“甲部门”人选有2人,“乙部门”人选有3人,由此利用列举法能求出至少有1人是“甲部门”人选的概率.
解答 解:(1)男生有14人,中间两个成绩是175和176,它们的平均数为175.5,
因此男生的成绩的中位数为175.5,
女生的平均成绩$\overline x=\frac{168+177+178+185+186+192}{6}=181$.
(2)用分层抽样的方法从“甲部门”和“乙部门”20人中抽5人,
每个人被抽到的概率是$\frac{5}{20}$=$\frac{1}{4}$,
根据茎叶图,“甲部门”人选有8人,“乙部门”人选有12人,
所以选中的“甲部门”人选有8×$\frac{1}{4}=2$人,“乙部门”人选有12×$\frac{1}{4}=3$人,
记选中的“甲部门”的人员为A1,A2,选中的“乙部门”人员为B,C,D,
从这5人中选2人的所有可能情况为:
(A1,A2),(A1,B),(A1,C),(A1,D),(A2,B),
(A2,C),(A2,D),(B,C),(B,D),(C,D)共10种,
其中至少有1人是“甲部门”人选的结果有7种,
∴至少有1人是“甲部门”人选的概率是$\frac{7}{10}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{7}$ | C. | $-\frac{1}{7}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,Q是棱CC1上的动点,则当BQ+D1Q的长度取得最小值时,直线B1Q和直线BD所成的角的正切值是$\frac{\sqrt{5}}{2}$.
在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,Q是棱CC1上的动点,则当BQ+D1Q的长度取得最小值时,直线B1Q和直线BD所成的角的正切值是$\frac{\sqrt{5}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
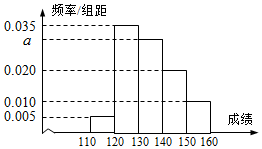 从高三年级随机抽取200名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为60.
从高三年级随机抽取200名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为60.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 18 | 19 | 20 | 21 | 22 |
| 销量y(册) | 61 | 56 | 50 | 48 | 45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com