
| A. | 0 | B. | 4 | C. | -4 | D. | 2 |
分析 根据△ABC的三边长度即可判断出△ABC为直角三角形,∠C=90°,从而可以求出$\overrightarrow{BC}•\overrightarrow{CA}=0$,而根据数量积的运算及向量加法的几何意义即可求出$\overrightarrow{AB}•\overrightarrow{BC}+\overrightarrow{CA}•\overrightarrow{AB}=-{\overrightarrow{AB}}^{2}=-4$,从而便可求出$\overrightarrow{AB}•\overrightarrow{BC}+\overrightarrow{BC}•\overrightarrow{CA}+\overrightarrow{CA}•\overrightarrow{AB}$的值.
解答 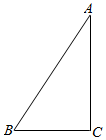 解:如图,
解:如图,
根据条件,AB2=BC2+AC2;
∴∠C=90°;
∴$\overrightarrow{BC}⊥\overrightarrow{CA}$;
∴$\overrightarrow{BC}•\overrightarrow{CA}=0$;
又$\overrightarrow{AB}•\overrightarrow{BC}+\overrightarrow{CA}•\overrightarrow{AB}=(\overrightarrow{BC}+\overrightarrow{CA})•\overrightarrow{AB}$=$\overrightarrow{BA}•\overrightarrow{AB}=-{\overrightarrow{AB}}^{2}=-4$;
∴$\overrightarrow{AB}•\overrightarrow{BC}+\overrightarrow{BC}•\overrightarrow{CA}+\overrightarrow{CA}•\overrightarrow{AB}=-4$.
故选:C.
点评 考查直角三角形边的关系,向量垂直的充要条件,以及向量数量积的运算,向量加法的几何意义,相反向量的概念.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:填空题
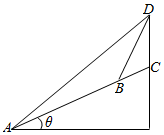 如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.
如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在四边形ABCD中,cosB=$\frac{\sqrt{3}}{3}$,∠D=2∠B,AD=1,且△ACD的面积为$\sqrt{2}$
如图所示,在四边形ABCD中,cosB=$\frac{\sqrt{3}}{3}$,∠D=2∠B,AD=1,且△ACD的面积为$\sqrt{2}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $-\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{n}^{2}+n}{2}$ | B. | $\frac{{n}^{2}-n}{2}$ | C. | $\frac{{n}^{2}+n-2}{2}$ | D. | n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | (2,3] | C. | (1,2) | D. | [1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com