Question

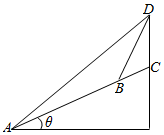
19．如图所示，在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD，为了测量该山坡相对于水平地面的坡角θ，在山坡的A处测得∠DAC=15°，沿山坡前进50m到达B处，又测得∠DBC=45°，根据以上数据可得cosθ=$\sqrt{3}$-1．

Answer 1

分析 在△ABD中，由正弦定理解出BD，在△BCD中，由正弦定理解出sin∠BCD，则cosθ=sin（π-∠BCD）=sin∠BCD．

解答 解：∵∠DAC=15°，∠DBC=45°，∴∠ADB=30°，
在△ABD中，由正弦定理得$\frac{AB}{sin∠ADB}=\frac{BD}{sin∠BAD}$，即$\frac{50}{\frac{1}{2}}=\frac{BD}{\frac{\sqrt{6}-\sqrt{2}}{4}}$，
∴BD=25（$\sqrt{6}-\sqrt{2}$）．
在△BCD中，由正弦定理得$\frac{CD}{sin∠DBC}=\frac{BD}{sin∠BCD}$，即$\frac{25}{\frac{\sqrt{2}}{2}}=\frac{25（\sqrt{6}-\sqrt{2}）}{sin∠BCD}$，
∴sin∠BCD=$\sqrt{3}-1$．
∴cosθ=sin（π-∠BCD）=sin∠BCD=$\sqrt{3}-1$．
故答案为：$\sqrt{3}-1$．

点评 本题考查了正弦定理，解三角形的应用，属于中档题．