
分析 由y=$\frac{3x+1}{x+a}$(a$≠\frac{1}{3}$),可得反函数:y=$\frac{-ax+1}{x-3}$,利用函数f(x)=$\frac{3x+1}{x+a}$(a$≠\frac{1}{3}$)图象与它的反函数图象重合,即为同一个函数即可得出.
解答 解:由y=$\frac{3x+1}{x+a}$(a$≠\frac{1}{3}$),解得x=$\frac{ay-1}{3-y}$(y≠3),把x与y互换可得:y=$\frac{ax-1}{3-x}$=$\frac{-ax+1}{x-3}$,
∵函数f(x)=$\frac{3x+1}{x+a}$(a$≠\frac{1}{3}$)图象与它的反函数图象重合,
∴-a=3,解得a=-3.
故答案为:-3.
点评 本题考查了反函数的求法及其性质,考查了推理能力与计算能力,属于中档题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
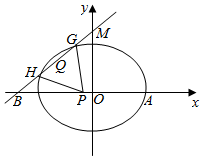 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点A(2,0),离心率$e=\frac{1}{2}$,斜率为k(0<k≤1)直线l过点M(0,2),与椭圆C交于G,H两点(G在M,H之间),与x轴交于点B.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点A(2,0),离心率$e=\frac{1}{2}$,斜率为k(0<k≤1)直线l过点M(0,2),与椭圆C交于G,H两点(G在M,H之间),与x轴交于点B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 75.5 | C. | 112.5 | D. | 225 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
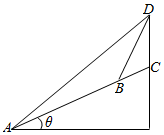 如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.
如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com