
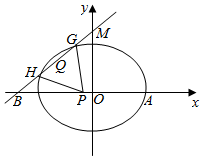
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点A(2,0),离心率$e=\frac{1}{2}$,斜率为k(0<k≤1)直线l过点M(0,2),与椭圆C交于G,H两点(G在M,H之间),与x轴交于点B.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点A(2,0),离心率$e=\frac{1}{2}$,斜率为k(0<k≤1)直线l过点M(0,2),与椭圆C交于G,H两点(G在M,H之间),与x轴交于点B.分析 (Ⅰ)由椭圆过点A(2,0),离心率$e=\frac{1}{2}$,求出a,b,c,由此能求出椭圆C的标准方程.
(Ⅱ)设G(x1,y1),H(x2,y2),直线l:y=kx+2. 由$\left\{\begin{array}{l}y=kx+2\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$得:(3+4k2)x2+16kx+4=0,由此利用韦达定理、弦长公式、三角形面积公式、椭圆性质,结合已知能求出$\frac{S_1}{S_2}$的取值范围.
解答 (本小题共13分)
解:(Ⅰ)∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点A(2,0),离心率$e=\frac{1}{2}$,
∴由已知得a=2,…(1分)
$e=\frac{c}{a}=\frac{1}{2}$,∴c=1,…(2分)
∴$b=\sqrt{3}$,…(3分)
∴椭圆C的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
(Ⅱ)设G(x1,y1),H(x2,y2),直线l:y=kx+2. …(5分)
由$\left\{\begin{array}{l}y=kx+2\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$得:(3+4k2)x2+16kx+4=0…(6分)
∴${x_1}+{x_2}=\frac{-16k}{{3+4{k^2}}},{x_1}•{x_2}=\frac{4}{{3+4{k^2}}}$,${y_1}+{y_2}=k({x_1}+{x_2})+4=\frac{12}{{3+4{k^2}}}$
即$Q(-\frac{8k}{{3+4{k^2}}},\frac{6}{{3+4{k^2}}})$…(7分)
∵△=16(12k2-3)>0,∴${k^2}>\frac{1}{4}$,即$k>\frac{1}{2}$.
∵0<k≤1,∴$\frac{1}{2}<k≤1$.…(8分)
又$\frac{S_1}{S_2}=\frac{{{S_{△PGH}}}}{{{S_{△PBQ}}}}=\frac{|GH|}{|BQ|}$,
而$|BQ|=\sqrt{{{(-\frac{2}{k}+\frac{8k}{{4{k^2}+3}})}^2}+{{(\frac{-6}{{4{k^2}+3}})}^2}}$=$\frac{{6\sqrt{1+{k^2}}}}{{(4{k^2}+3)k}}$,…(9分)
$|GH|=\sqrt{1+{k^2}}\frac{{4\sqrt{12{k^2}-3}}}{{4{k^2}+3}}$,…(10分)
$\frac{S_1}{S_2}=\frac{|GH|}{|BQ|}$=$\frac{{2\sqrt{3}}}{3}\sqrt{4{k^4}-{k^2}}$,…(11分)
∵$\frac{1}{4}<{k^2}≤1$设$t={k^2},(\frac{1}{4}<t≤1)$$\frac{S_1}{S_2}=\frac{{2\sqrt{3}}}{3}\sqrt{4{t^2}-t}$,
∴$\frac{S_1}{S_2}∈({0,2}]$.即 $\frac{S_1}{S_2}$的取值范围是(0,2].…(13分)
点评 本题考查椭圆方程的求法,考查两三角形面积比值的取值范围的求法,是中档题,解题时要认真审题,注意韦达定理、弦长公式、三角形面积公式、椭圆性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的长轴长是短轴长的两倍,焦距为2$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的长轴长是短轴长的两倍,焦距为2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com