
| A. | 1 | B. | 2 | C. | 2016 | D. | 2018 |
分析 正项等差数列{an}满足a1+a2017=2,可得a2+a2016=a1+a2017=2,化简利用基本不等式的性质即可得出.
解答 解:∵正项等差数列{an}满足a1+a2017=2,
∴a2+a2016=a1+a2017=2,
则$\frac{1}{a_2}+\frac{1}{{{a_{2016}}}}$=$\frac{{a}_{2}+{a}_{2016}}{{a}_{2}{a}_{2016}}$=$\frac{2}{{a}_{2}{a}_{2016}}$≥$\frac{2}{(\frac{{a}_{1}+{a}_{2017}}{2})^{2}}$=2,当且仅当a1=a2017时取等号.
故选:B.
点评 本题考查了等差数列的通项公式性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点到直线x-y+3$\sqrt{2}$=0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为$\sqrt{10}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点到直线x-y+3$\sqrt{2}$=0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为$\sqrt{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 75.5 | C. | 112.5 | D. | 225 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
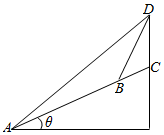 如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.
如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在四边形ABCD中,cosB=$\frac{\sqrt{3}}{3}$,∠D=2∠B,AD=1,且△ACD的面积为$\sqrt{2}$
如图所示,在四边形ABCD中,cosB=$\frac{\sqrt{3}}{3}$,∠D=2∠B,AD=1,且△ACD的面积为$\sqrt{2}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com