
分析 通过Sn=$\frac{1}{2}$anan+1,利用an+1=Sn+1-Sn化简可知数列{an}的通项公式,进而裂项可知$\frac{1}{2{S}_{n}}$=$\frac{1}{n}$-$\frac{1}{n+1}$,并项相加、比较即得结论.
解答 解:∵Sn=$\frac{1}{2}$anan+1,
∴an+1=Sn+1-Sn=$\frac{1}{2}$an+1an+2-$\frac{1}{2}$anan+1,
整理得:an+2-an=2,
又∵a1=1,a2=$\frac{2{S}_{1}}{{a}_{1}}$=2,
∴数列{an}的通项公式an=n,
∴$\frac{1}{2{S}_{n}}$=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
又∵Tn=$\frac{99}{100}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$,
∴n=99,
故答案为:99.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
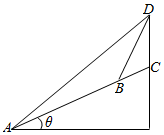 如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.
如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1 | ||
| C. | $\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1和$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1或$\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在四边形ABCD中,cosB=$\frac{\sqrt{3}}{3}$,∠D=2∠B,AD=1,且△ACD的面积为$\sqrt{2}$
如图所示,在四边形ABCD中,cosB=$\frac{\sqrt{3}}{3}$,∠D=2∠B,AD=1,且△ACD的面积为$\sqrt{2}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com