
分析 将意义及条件进行转化,可得a≥$\frac{|x+1|}{|x-1|+|x+3|}$,再结合|x-1|+|x+3|≥2|x+1|,即可求出a的取值范围,注意等号成立的条件
解答 解:若f(x)≤a|x+3|,则|x+1|-a|x-1|≤a|x+3|,
即|x+1|≤a(|x-1|+|x+3|),
即a≥$\frac{|x+1|}{|x-1|+|x+3|}$,
由|x-1|+|x+3|≥2|x+1|,
∴$\frac{|x+1|}{|x-1|+|x+3|}$≤$\frac{|x+1|}{2|x+1|}$=$\frac{1}{2}$,当且仅当x≥1或x≤-3时取等号,
即a≥$\frac{1}{2}$,则a的取值范围是a≥$\frac{1}{2}$
即a的最小值为$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 本题考查绝对值不等式的应用,以及恒成立的问题,考查了学生的转化能力和运算能力,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
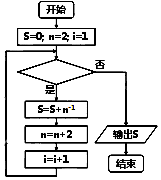
| A. | i>10 | B. | i<10 | C. | i<20 | D. | i>20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
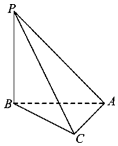 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )| A. | 3π | B. | 5π | C. | 12π | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $d≈\root{3}{{\frac{60}{31}V}}$ | B. | $d≈\root{3}{2V}$ | C. | $d≈\root{3}{{\frac{15}{8}V}}$ | D. | $d≈\root{3}{{\frac{21}{11}V}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com