
分析 (1)推导出cosC=1-2sin2$\frac{C}{2}$=-$\frac{1}{4}$,从而sinC=$\frac{\sqrt{15}}{4}$,由此利用余弦函数加法定理能求出cos(C+$\frac{π}{6}$).
(2)由△ABC的面积是$\frac{3\sqrt{15}}{4}$,求出ab=6,由正弦定理得${a}^{2}+{b}^{2}=\frac{13}{16}{c}^{2}$,由此利用余弦定理能求出c.
解答 解:(1)∵在△ABC中,角A,B,C所对的边分别为a,b,c,sin$\frac{C}{2}$=$\frac{\sqrt{10}}{4}$.
∴cosC=1-2sin2$\frac{C}{2}$=1-2×($\frac{\sqrt{10}}{4}$)2=1-$\frac{5}{4}$=-$\frac{1}{4}$,
sinC=$\sqrt{1-(-\frac{1}{4})^{2}}$=$\frac{\sqrt{15}}{4}$,
∴cos(C+$\frac{π}{6}$)=cosCcos$\frac{π}{6}$-sinCsin$\frac{π}{6}$
=-$\frac{1}{4}×\frac{\sqrt{3}}{2}$-$\frac{\sqrt{15}}{4}×\frac{1}{2}$=-$\frac{\sqrt{3}+\sqrt{15}}{8}$.
(2)∵△ABC的面积是$\frac{3\sqrt{15}}{4}$,
∴${S}_{△ABC}=\frac{1}{2}absinC=\frac{1}{2}ab×\frac{\sqrt{15}}{4}$=$\frac{3\sqrt{15}}{4}$,解得ab=6,
∵$si{n}^{2}A+si{n}^{2}B=\frac{13}{16}si{n}^{2}C$,即${a}^{2}+{b}^{2}=\frac{13}{16}{c}^{2}$,
由余弦定理得:c2=a2+b2-2abcosC=$\frac{13}{16}{c}^{2}-2×6×(-\frac{1}{4})$=$\frac{13}{16}{c}^{2}$+3,
解得c=4.
点评 本题考查三角函值和三角形边长的求法,涉及到正弦定理、余弦定理、同角三角函数关系式、余弦函数加法定理等基础知识,考查推理论证能力、运算求解能力,考查函数与方思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π-2 | B. | 2π-4 | C. | 3π-6 | D. | 4π-8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
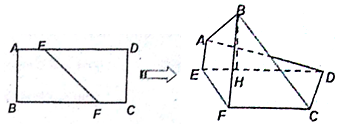
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
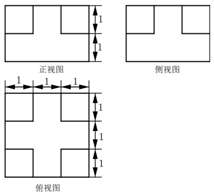 榫卯(sǔn mǎo)是古代中国建筑、家具及其它器械的主要结构方式,是在两个构件上采用凹凸部位相结合的一种连接方式,凸出部分叫做“榫头”.某“榫头”的三视图及其部分尺寸如图所示,则该“榫头”体积等于( )
榫卯(sǔn mǎo)是古代中国建筑、家具及其它器械的主要结构方式,是在两个构件上采用凹凸部位相结合的一种连接方式,凸出部分叫做“榫头”.某“榫头”的三视图及其部分尺寸如图所示,则该“榫头”体积等于( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com