
| A. | π-2 | B. | 2π-4 | C. | 3π-6 | D. | 4π-8 |
分析 根据函数的奇偶性得到函数的周期是2π,分别求出函数的解析式,利用积分的应用即可得到结论.
解答 解:由f(π-x)=f(x)得f(x+π)=f(-x)=-f(x),
当0≤x≤$\frac{π}{2}$,由已知得到f(x)=cosx-1,
∵f(x)是R上的奇函数,
∴当$\frac{π}{2}$<x≤π时,0<π-x≤$\frac{π}{2}$,
所以由f(π-x)=f(x)=cos(π-x)-1=-cosx-1,
所以f(x)=$\left\{\begin{array}{l}{cosx-1,0≤x≤\frac{π}{2}}\\{-cosx-1,\frac{π}{2}<x≤π}\end{array}\right.$,
所以当0≤x≤π时,f(x)的图象与x轴所围成图形的面积-${∫}_{0}^{\frac{π}{2}}(cosx-1)dx+{∫}_{\frac{π}{2}}^{π}(-cosx-1)dx$=${∫}_{0}^{\frac{π}{2}}(1-cosx)dx+{∫}_{\frac{π}{2}}^{π}(cosx+1)dx$=(x-sinx)|${\;}_{0}^{\frac{π}{2}}$+(sinx+x)|${\;}_{\frac{π}{2}}^{π}$=π-2;
故选A.
点评 本题主要考查利用积分求面积,根据函数的奇偶性和周期性分别求出对应的解析式是解决本题的关键.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $d≈\root{3}{{\frac{60}{31}V}}$ | B. | $d≈\root{3}{2V}$ | C. | $d≈\root{3}{{\frac{15}{8}V}}$ | D. | $d≈\root{3}{{\frac{21}{11}V}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
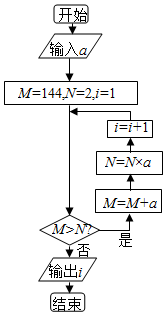 执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )
执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )| A. | [9,+∞) | B. | [8,9] | C. | [8,144) | D. | [9,144) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com