
分析 (Ⅰ)由正弦定理推导出$\sqrt{3}cosBsinC=sinBsinC$,从而$tanB=\sqrt{3}$,由此能求出角B.
(Ⅱ)由$\frac{a}{sinA}=\frac{c}{sinC}=\frac{b}{sinB}=\frac{4}{{\sqrt{3}}}$,得$a=\frac{4}{{\sqrt{3}}}sinA$,$c=\frac{4}{{\sqrt{3}}}sinC$,由此利用正弦函数加法定理能求出a+c的取值范围.
解答 解:(Ⅰ)在△ABC中,∵$\sqrt{3}a=b(sinC+\sqrt{3}cosC)$,
∴$\sqrt{3}sinA=sinB(sinC+\sqrt{3}cosC)$$\sqrt{3}sin(B+C)=sinB(sinC+\sqrt{3}cosC)$,
∴$\sqrt{3}cosBsinC=sinBsinC$,
∵sinC>0.
∴$\sqrt{3}cosB=sinB$,即$tanB=\sqrt{3}$…(4分)
而B∈(0,π),则$B=\frac{π}{3}$. …(6分)
(Ⅱ) 由$\frac{a}{sinA}=\frac{c}{sinC}=\frac{b}{sinB}=\frac{4}{{\sqrt{3}}}$得$a=\frac{4}{{\sqrt{3}}}sinA$,$c=\frac{4}{{\sqrt{3}}}sinC$
∴$a+c=\frac{4}{{\sqrt{3}}}(sinA+sinC)=\frac{4}{{\sqrt{3}}}[sinA+sin(\frac{2π}{3}-A)]$=$\frac{4}{{\sqrt{3}}}(\frac{3}{2}sinA+\frac{{\sqrt{3}}}{2}cosA)=4sin(A+\frac{π}{6})$…(9分)
∵$A∈(0,\frac{2π}{3})$,∴$A+\frac{π}{6}∈(\frac{π}{6},\frac{5π}{6})$
∴$sin(A+\frac{π}{6})∈(\frac{1}{2},1]$
∴a+c∈(2,4]…(12分)
点评 本题考查三角形的角的求法,考查两边边长和的取值范围的求法,涉及到正弦定理、余弦定理、同角三角函数关系式、正弦函数加法定理等基础知识,考查推理论证能力、运算求解能力,考查函数与方思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:选择题
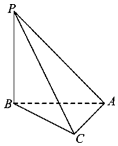 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )| A. | 3π | B. | 5π | C. | 12π | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
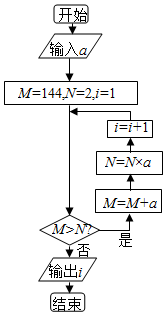 执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )
执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )| A. | [9,+∞) | B. | [8,9] | C. | [8,144) | D. | [9,144) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
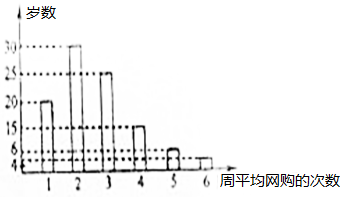 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.| 网购迷 | 非网购迷 | 合计 | |
| 年龄不超过40岁 | |||
| 年龄超过40岁 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com