练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．解不等式组：$\left\{\begin{array}{l}{\frac{5}{x+3}≥1}\\{{x}^{2}+x-2≥0}\end{array}\right.$．

    分析 首先将分式不等式转化为整式不等式，把二次不等式分解，分别求出x 范围，取交集即可．

    解答 解：原不等式组即：$\left\{\begin{array}{l}{0＜x+3≤5}\\{（x+2）（x-1）≥0}\end{array}\right.$，所以$\left\{\begin{array}{l}{-3＜x≤2}\\{x≤-2，或x≥1}\end{array}\right.$，
    所以-3＜x≤-2，或1≤x≤2，
    故原不等式组的解集为{x|-3＜x≤-2，或1≤x≤2}．

    点评 本题考查了由分式不等式以及一元二次不等式组成的不等式组的解法；关键是正确转化为整式不等式解之．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    7．已知曲线C1，C2的极坐标方程分别为ρ=2cosθ，$\sqrt{2}ρsin（θ-\frac{π}{4}）=\frac{{\sqrt{3}}}{2}$，射线θ=φ，$θ=φ+\frac{π}{4}$，$θ=φ-\frac{π}{4}$与曲线C1交于（不包括极点O）三点A，B，C．
    （Ⅰ）求证：$|OB|+|OC|=\sqrt{2}|OA|$；
    （Ⅱ）当$φ=\frac{π}{12}$时，求点B到曲线C2上的点的距离的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知函数y=f（x）的图象关于x=1对称，且在（1，+∞）上单调递增，设$a=f（\frac{1}{2}）$，b=f（2），c=f（3），则a，b，c的大小关系为（　　）
    A．b＜a＜cB．c＜b＜aC．b＜c＜aD．a＜b＜c

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数$f（x）=2\sqrt{3}sinωxcosωx-2{cos^2}ωx+1（ω＞0）$，且y=f（x）的图象与直线y=2的两个相邻公共点之间的距离为π．
    （1）求函数f（x）的解析式，并求出f（x）的单调递增区间；
    （2）将函数f（x）的图象上所有点向左平移$\frac{π}{6}$个单位，得到函数g（x）的图象，设A，B，C为△ABC的三个内角，若g（B）-2=0，且向量$\overrightarrow m=（cosA，cosB）$，$\overrightarrow n=（1，sinA-cosAtanB）$，求$\overrightarrow m•\overrightarrow n$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

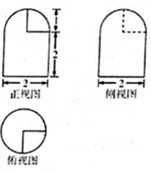    12．已知一个几何体的三视图如图所示，则该几何体的表面积为（　　）
    A．$\frac{25}{4}$πB．7πC．$\frac{29}{4}$πD．$\frac{31}{4}$π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．如图是某学校某年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象，为了容易看出一个班级的成绩变化，将离散的点用虚线连接，根据图象，给出下列结论：
    ①一班成绩始终高于年级平均水平，整体成绩比较好；
    ②二班成绩不够稳定，波动程度较大；
    ③三班成绩虽然多数时间低于年级平均水平，但在稳步提升．
    其中正确结论的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知m＞0，n＞0，则当81m2+n2+$\frac{729}{8mn}$取得最小值时，m-n的值为（　　）
    A．-4B．4C．-8D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．若集合A={x||2x|＞1}，B={x|2x2-x-1＜0}，则A∩B=（　　）
    A．{x|-1＜x＜2}B．$\left\{{x\left|{\frac{1}{2}＜x＜1}\right.}\right\}$C．$\left\{{x\left|{-\frac{1}{2}＜x＜1}\right.}\right\}$D．{x|x＞1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．在极坐标系中，曲线C的方程为$ρ=4cosθ+2sinθ-\frac{3}{ρ}$，以极点O为原点，极轴为x轴的正半轴建立平面直角坐标系．
    （Ⅰ）求曲线C的参数方程；
    （Ⅱ）在直角坐标系中，点M（x，y）是曲线C上一动点，求x+y的最大值，并求此时点M的直角坐标．

    查看答案和解析>>

    同步练习册答案