
分析 (Ⅰ)首先把曲线转化为:ρ2=4ρcosθ+2ρsinθ-3,整理得:(x-2)2+(y-1)2=2.进一步转化为参数方程为:$\left\{\begin{array}{l}{x=2+\sqrt{2}cosθ}\\{y=1+\sqrt{2}sinθ}\end{array}\right.$(θ为参数).
(Ⅱ)根据(Ⅰ)所得的参数方程,进一步利用三角函数的恒等变换变换成正弦型三角函数,最后求出函数关系式的最值及坐标.
解答 解:(Ⅰ)曲线C的方程为$ρ=4cosθ+2sinθ-\frac{3}{ρ}$,转化为:ρ2=4ρcosθ+2ρsinθ-3,
整理得:(x-2)2+(y-1)2=2.
进一步转化为参数方程为:$\left\{\begin{array}{l}{x=2+\sqrt{2}cosθ}\\{y=1+\sqrt{2}sinθ}\end{array}\right.$(θ为参数).
(Ⅱ)由(Ⅰ)得:
x+y=$3+\sqrt{2}(sinθ+cosθ)$,
=$3+2sin(θ+\frac{π}{4})$,
当且仅当$θ=\frac{π}{4}$时,(x+y)max=5.
M(3,2)为取得最大值时的坐标.
点评 本题考查的知识点:极坐标方程与参数方程和普通方程的互化,三角函数关系式的恒等变换,三角函数的最值,属于基础题型.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 0<f'(3)<f'(4)<f(4)-f(3) | B. | 0<f(4)-f(3)<f'(3)<f'(4) | C. | 0<f'(4)<f'(3)<f(4)-f(3) | D. | 0<f'(4)<f(4)-f(3)<f'(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | D2+E2-4F>0,且F<0 | B. | D<0,F>0 | ||
| C. | D≠0,F≠0 | D. | F<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16f(-3)>9f(4) | B. | 16f(3)<9f(-4) | C. | 9f(3)>16f(4) | D. | 9f(-3)<16f(-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )
在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )| A. |  | B. |  | C. |  | D. | 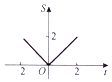 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com