已知不等式
+
+…+
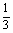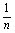>[log2n],其中n为大于2的整数，[log2n]表示不超过log2n的最大整数。设数列{an}的各项为正，且满足a1=b(b>0),an≤
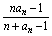,n=2,3,4,….(Ⅰ)证明：an≤
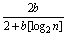，n=2,3,4,5,…;
(Ⅱ)猜测数列{an}是否有极限？如果有，写出极限的值（不必证明）；
（Ⅲ）试确定一个正整数N，使得当n>N时，对任意b>0,都有an<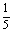
.
阅读快车系列答案科目：高中数学 来源： 题型：
对于等差数列{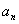
}，有如下一个真命题：“若{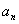}是等差数列，且
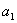＝0，s、t是互不相等的正整数，则
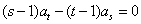”．类比此命题，对于等比数列{
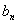}，有如下一个真命题：若{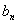}是等比数列，且
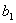＝1，s、t是互不相等的正整数，则 .
查看答案和解析>>
科目：高中数学 来源： 题型：
已知数列{an}是首项为-1，公差d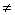 
0的等差数列，且它的第2、3、6项依次构成等比数列{ bn}的前3项。
(1)求{an}的通项公式；(2)若Cn=an·bn，求数列{Cn}的前n项和Sn。
查看答案和解析>>
科目：高中数学 来源： 题型：
在数列{an}（n∈N*）中，已知a1＝1，a2k＝－ak，a2k－1＝(－1)k+1ak，k∈N*. 记数列{an}的前n项和为Sn.
（1）求S5，S7的值；（2）求证：对任意n∈N*，Sn≥0.
查看答案和解析>>
科目：高中数学 来源： 题型：
已知数列{an}的前n项和Sn=a[2-(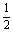
)n-1]-b[2-(n+1)(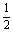)n-1](n=1,2,…),其中a,b是非零常数,则存在数列{xn}、{yn}使得（ ）
A.an=xn+yn,其中{xn}为等差数列，{yn}为等比数列B．an=xn+yn,其中{xn}和{yn}都为等差数列
C．an=xn·yn,其中{xn}为等差数列，{yn}为等比数列D．an=xn·yn,其中{xn}和{yn}都为等比数列
查看答案和解析>>
科目：高中数学 来源： 题型：
平面上点P与不共线的三点A、B、C满足关系：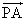
＋
＋
＝
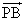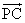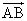，则下列结论正确的是( )
(A)P在CA上，且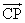
＝2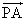 (B)P在AB上，且
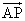＝2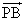
(B)(C)P在BC上，且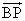
＝2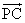 (D)P点为△ABC的重心
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
∴
,于是有
中，
，则
等于
＝_________ (n∈N*)．
，
，数列
满足
，则数列
等于________