在数列{an}（n∈N*）中，已知a1＝1，a2k＝－ak，a2k－1＝(－1)k+1ak，k∈N*. 记数列{an}的前n项和为Sn.
（1）求S5，S7的值；（2）求证：对任意n∈N*，Sn≥0.
科目：高中数学 来源： 题型：
如图所示，∠AOB=1rad，点Al，A2，…在OA上，点B1，B2，…在OB上，其中的每一个实线段和虚线段的长均为1个长度单位，一个动点M从O点出发，沿着实线段和以O为圆心的圆弧匀速运动，速度为l长度单位／秒，则质点M到达A3点处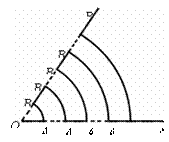
所需要的时间为__秒，质点M到达An点处所需要的时间为 秒．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知不等式
+
+…+
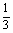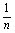>[log2n],其中n为大于2的整数，[log2n]表示不超过log2n的最大整数。设数列{an}的各项为正，且满足a1=b(b>0),an≤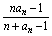
,n=2,3,4,….(Ⅰ)证明：an≤
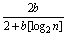，n=2,3,4,5,…;
(Ⅱ)猜测数列{an}是否有极限？如果有，写出极限的值（不必证明）；
（Ⅲ）试确定一个正整数N，使得当n>N时，对任意b>0,都有an<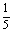
.
查看答案和解析>>
科目：高中数学 来源： 题型：
设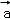
，
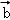是两个非零向量（ ）
|
| A． | 若| | B． | 若 |
|
| C． | 若| | D． | 若存在实数λ，使得 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
故有
故可知S5＝3，S7＝1. 2分
首项为
，公差为
，等比数列
首项为
都是大于1的正整数，且
，对于任意的
，总存在
，使得
成立，则
中，前n项和为
，且
．（Ⅰ）求数列
，数列
前n项和为
，求
是首项为1，公比为2的等比数列，那么an = （ ） A．2n+1－1 B．2n－1 C．2n－1 D．2n +1
的前
项和为
，且
，
，则过点
和
的直线的一个方向向量的坐标可以是（ ）A．
B．
C．
D．
+
|=|
|﹣|
|
，则|
|=|