
分析 (1)将a=2代入,分别解出不同情况满足不等式f(x)<x的x值,综合可得答案;
(2)分别求解不同情况下满足不等式f(x)<2a2的x值,综合可得答案;
解答 解:(1)当a=2时,不等式f(x)<x可化为:
$\left\{\begin{array}{l}x(x-2)<x,x≥2\\ x(2-x)<x,x<2\end{array}\right.$
解得:x∈(-∞,0)∪(1,3);
(2)当a>0时,2a>a,
等式f(x)<2a2可化为:
$\left\{\begin{array}{l}x(x-a)<2{a}^{2},x≥a\\ x(a-x)<2{a}^{2},x<a\end{array}\right.$,
当x≥a时,不等式可化为:x2-ax-2a2<0,
解得:-a<x<2a,
∴a≤x<2a,
当x<a时,不等式可化为:x2-ax+2a2>0,
此时不等式恒成立,
∴x<a,
综上可得:原不等式的解集为(-∞,2a)
点评 本题考查的知识点是分段函数的应用,二次不等式的解法,二次函数的图象和性质,难度中档.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
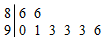 如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )| A. | 93,91 | B. | 86,93 | C. | 93,92 | D. | 86,91 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加 | 不参加 | 待定 | |
| 文科生 | 120 | 300 | 180 |
| 理科生 | 780 | 200 | 420 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 完成时间 | 频率 |
| [20,25) | 0.2 |
| [25,30) | 0.5 |
| [30,35) | 0.2 |
| [35,40) | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com