
分析 (1)由已知,$\frac{c}{a}=\frac{{\sqrt{3}}}{2},\frac{1}{2}ab=1$,又a2=b2+c2,解出即可得出.
(2)设直线l的方程为y=2x+t,则$\left\{\begin{array}{l}\frac{x^2}{4}+{y^2}=1\\ y=2x+t\end{array}\right.$,可得$(4{t^2}-4){({\frac{y}{x}})^2}+16({\frac{y}{x}})+({t^2}-16)=0$,根据OP⊥OQ,可得kOP•kOQ=-1,解出即可得出.
(3)设E(m,0)、M(x1,y1)、N(x2,y2),当直线n不为x轴时的方程为x=ty+m,与椭圆方程联立化为(t2+4)y2+2tmy+(m2-4)=0,利用根与系数的关系可得:$\frac{1}{{|EM{|^2}}}+\frac{1}{{|EN{|^2}}}$为定值5.
解答 解:(1)由已知,$\frac{c}{a}=\frac{{\sqrt{3}}}{2},\frac{1}{2}ab=1$,又a2=b2+c2,解得$a=2,b=1,c=\sqrt{3}$,
∴椭圆的方程为$\frac{x^2}{4}+{y^2}=1$.…(3分)
(2)设直线l的方程为y=2x+t,则由$\left\{\begin{array}{l}\frac{x^2}{4}+{y^2}=1\\ y=2x+t\end{array}\right.$,可得$\frac{x^2}{4}+{y^2}={({\frac{y-2x}{t}})^2}$,
即$(4{t^2}-4){({\frac{y}{x}})^2}+16({\frac{y}{x}})+({t^2}-16)=0$
∵OP⊥OQ,∴$\frac{{{t^2}-16}}{{4{t^2}-4}}=-1⇒{t^2}=4⇒t=±2$,
∴直线l的方程为y=2x±2即2x-y±2=0.…(7分)
(3)设E(m,0)、M(x1,y1)、N(x2,y2),当直线n不为x轴时的方程为x=ty+m,
联立椭圆方程得:$\left\{\begin{array}{l}x=ty+m\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$⇒(t2+4)y2+2tmy+(m2-4)=0,∴${y_1}+{y_2}=-\frac{2tm}{{{t^2}+4}},{y_1}{y_2}=\frac{{{m^2}-4}}{{{t^2}+4}}$…(8分)
$\frac{1}{{|EA{|^2}}}+\frac{1}{{|EB{|^2}}}=\frac{1}{{(1+{t^2})y_1^2}}+\frac{1}{{(1+{t^2})y_2^2}}=\frac{1}{{(1+{t^2})}}•\frac{{{{({y_1}+{y_2})}^2}-2{y_1}{y_2}}}{y_1^2y_2^2}$=$\frac{1}{{1+{t^2}}}•\frac{{(32-8{m^2})+(2{m^2}+8){t^2}}}{{{{({m^2}-4)}^2}}}$…(10分)
∴当且仅当32-8m2=2m2+8即$m=±\frac{{2\sqrt{15}}}{5}$时$\frac{1}{{|EA{|^2}}}+\frac{1}{{|EB{|^2}}}=5$(定值).
即 在x轴上存在点E使得$\frac{1}{{|EA{|^2}}}+\frac{1}{{|EB{|^2}}}$为定值5,点E的坐标为$({\frac{{2\sqrt{15}}}{3},0})$或$({-\frac{{2\sqrt{15}}}{3},0})$. 经检验,当直线AB为x轴时上面求出的点E也符合题意.…(12分)
点评 本题考查了椭圆的标准方程及其性质、相互垂直的直线斜率之间的关系、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
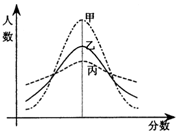 某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )
某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )| A. | 甲、乙、丙的总体的平均数不相同 | B. | 乙科总体的标准差及平均数都居中 | ||
| C. | 丙科总体的平均数最小 | D. | 甲科总体的标准差最小 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.20 | B. | 0.25 | C. | 0.30 | D. | 0.35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com