
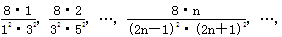 Sn为该数列的前n项和,计算得
Sn为该数列的前n项和,计算得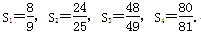
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源:不详 题型:解答题
 }的前n项和Sn= —a
}的前n项和Sn= —a —(
—( )
)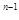 +2 (n为正整数).
+2 (n为正整数). =
= a
a + (
+ ( )
) .,并求数列{a
.,并求数列{a }的通项
}的通项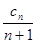 =
=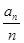 ,T
,T = c
= c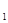 +c
+c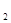 +···+c
+···+c ,求T
,求T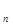 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 行共有
行共有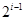 个正整数,设
个正整数,设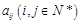 表示位于这个数表中从上往下数第
表示位于这个数表中从上往下数第 行,从左往右第
行,从左往右第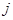 个数.
个数.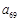 的值;
的值;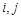 表示
表示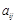 ;
;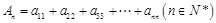 ,求证:当
,求证:当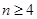 时,
时,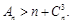
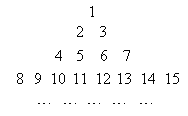
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 f(a1),f(
f(a1),f( a2),…,f(an)…(n∈N?)是首项为m2,公比为m的等比数列.
a2),…,f(an)…(n∈N?)是首项为m2,公比为m的等比数列. 出m的范围;若不存在,请说明理由.
出m的范围;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com