
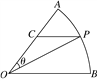
【题目】如图所示,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,当△POC面积的最大值时θ的值为___________
科目:高中数学 来源: 题型:
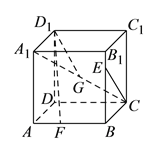
【题目】已知正方体![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 和
和![]() 上的动点,观察直线
上的动点,观察直线![]() 与
与![]() ,
, ![]() 与
与![]() .给出下列结论:
.给出下列结论:
①对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
②对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
③对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
④对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() .
.
其中正确结论的个数是( ).
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一缉私艇发现在方位角45°方向,距离12海里的海面上有一走私船正以10海里/小时的速度沿方位角为105°方向逃窜,若缉私艇的速度为14海里/小时,缉私艇沿方位角45°+α的方向追去,若要在最短的时间内追上该走私船,求追击所需时间和α角的正弦.(注:方位角是指正北方向按顺时针方向旋转形成的角,设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇). 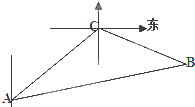
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
回归方程为 ![]() =bx+a,其中b=
=bx+a,其中b= 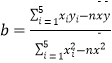 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,求出y与x的回归方程 ![]() =bx+a;
=bx+a;
(3)预测销售额为115万元时,大约需要多少万元广告费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是半圆
是半圆![]() 的直径,
的直径, ![]() 是半圆
是半圆![]() 上除
上除![]() 、
、![]() 外的一个动点,
外的一个动点, ![]() 垂直于半圆
垂直于半圆![]() 所在的平面,
所在的平面, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
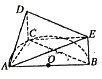
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲船在岛B的正南A处,AB=10千米.甲船以每小时4千米的速度向北航行,同时,乙船自B出发以每小时6千米的速度向北偏东60°的方向驶去.当甲船在A,B之间,且甲、乙两船相距最近时,它们所航行的时间是( )

A. ![]() 分钟 B.
分钟 B. ![]() 小时 C. 21.5分钟 D. 2.15分钟
小时 C. 21.5分钟 D. 2.15分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 为
为![]() 与
与![]() 交点,已知
交点,已知![]() ,
,![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅲ)设点![]() 在
在![]() 内(含边界),且
内(含边界),且![]()
![]() ,说明满足条件的点
,说明满足条件的点![]() 的轨迹,并求
的轨迹,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①![]() ,②
,②![]() 拟合,得到回归方程分别为
拟合,得到回归方程分别为![]() ,
, ![]() ,作残差分析,如表:
,作残差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于![]() 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为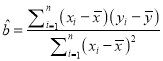 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com