
设数列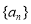 的前
的前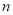 项和为
项和为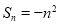 ,数列
,数列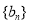 满足:
满足: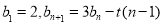 ,已知
,已知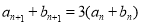 对任意
对任意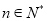 都成立
都成立
(1)求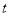 的值
的值
(2)设数列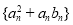 的前
的前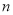 项的和为
项的和为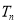 ,问是否存在互不相等的正整数
,问是否存在互不相等的正整数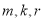 ,使得
,使得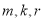 成等差数列,且
成等差数列,且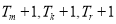 成等比数列?若存在,求出
成等比数列?若存在,求出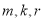 ;若不存在,说明理由
;若不存在,说明理由
(1)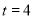 (2)不存在满足条件的正整数m,k,r,使得
(2)不存在满足条件的正整数m,k,r,使得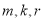 成等差数列,且
成等差数列,且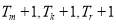 成等比数列.
成等比数列.
【解析】
试题分析:(1)先利用递推关系式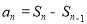 求出数列
求出数列 的通项,再利用
的通项,再利用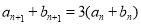 对任意
对任意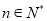 都成立,
都成立,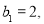 证明出数列
证明出数列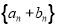 是首项为1,公比为3的等比数列并求出其通项然后
是首项为1,公比为3的等比数列并求出其通项然后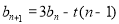
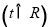 ,所以
,所以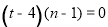 对任意
对任意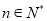 都成立,进而求出t的值;
都成立,进而求出t的值;
(2)由(1)得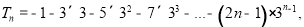 然后利用错位相减法解出
然后利用错位相减法解出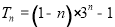
再由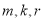 成等差数列,且
成等差数列,且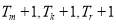 成等比数列.得m=r.这与
成等比数列.得m=r.这与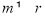 矛盾,所以,不存在满足条件的正整数m,k,r,
矛盾,所以,不存在满足条件的正整数m,k,r,
试题解析:(1)当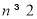 时,
时,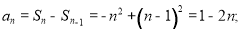
当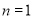 时,
时,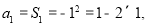 也适合上式.
也适合上式.
所以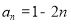 (
(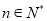 ) .2分
) .2分
因为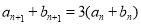 多任意
多任意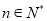 都成立,
都成立,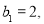
所以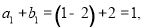
所以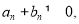 且
且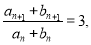
所以数列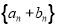 是首项为1,公比为3的等比数列.
是首项为1,公比为3的等比数列.
所以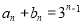 , ..4分
, ..4分
即
因为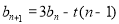
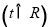 ,
,
所以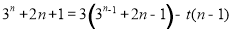
所以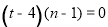 对任意
对任意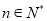 都成立,
都成立,
所以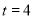 , 6分
, 6分
(2)由(1)得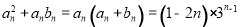 ,
,
所以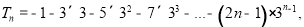
所以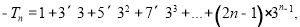
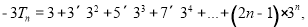
两式相减,得
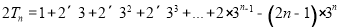
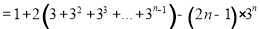
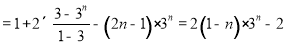
解得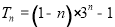 ..8分
..8分
若存在互不相等的正整数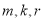 ,使得
,使得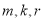 成等差数列,且
成等差数列,且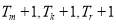 成等比数列.
成等比数列.
则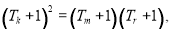
即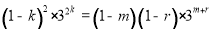 .
.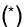
由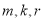 成等差数列,得
成等差数列,得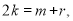 所以
所以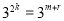 .
.
所以由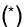 得
得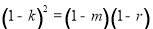 .
.
即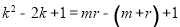
所以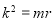
即 即
即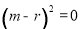 即m=r.
即m=r.
这与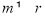 矛盾
矛盾
所以,不存在满足条件的正整数m,k,r, .10分
考点:等差等比数列的基本性质;等差等比数列的前n项和公式;错位相减法;探索型问题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源:2016届江苏省高一下学期期末模拟考试数学试卷(解析版) 题型:填空题
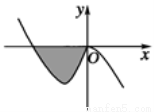
已知函数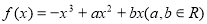 的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为
的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为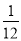 ,则
,则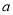 的值为 __.
的值为 __.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高一下学期期末模拟数学试卷2(解析版) 题型:填空题
已知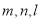 是直线,
是直线,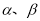 是平面,下列命题中,正确的命题是 .(填序号)
是平面,下列命题中,正确的命题是 .(填序号)
①若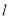 垂直于
垂直于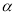 内两条直线,则
内两条直线,则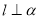 ;
;
②若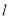 平行于
平行于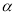 ,则
,则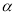 内可有无数条直线与
内可有无数条直线与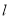 平行;
平行;
③若m⊥n,n⊥l则m∥l; ④若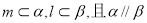 ,则
,则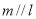 ;
;
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高一下学期期末模拟数学试卷1(解析版) 题型:填空题
在△ABC中,已知∠BAC=90°,AB=6,若D点在斜边BC上,CD=2DB,则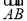 ·
·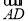 的值为 .
的值为 .
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高一下学期期中考试数学试卷(解析版) 题型:填空题
设等差数列{an}的前n项的和为Sn,若a1>0,S4=S8,则当Sn取最大值时,n的值为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com