
分析 利用诱导公式化简求解即可.
解答 解:sinα=$\frac{3}{5}$,则
①sin(180°-α)=sinα=$\frac{3}{5}$;
②sin(π+α)=-sinα=-$\frac{3}{5}$;
③sin(-α)=-sinα=-$\frac{3}{5}$;
④sin(7π-α)=sinα=$\frac{3}{5}$;
⑤cos(90°-α)=sinα=$\frac{3}{5}$;
⑥cos($\frac{π}{2}$+α)=-sinα=-$\frac{3}{5}$;
⑦cos($\frac{3π}{2}$+α)=sinα=$\frac{3}{5}$;
⑧cos(270°-α)=-sinα=-$\frac{3}{5}$.
故答案为:$\frac{3}{5}$;-$\frac{3}{5}$;-$\frac{3}{5}$;$\frac{3}{5}$;$\frac{3}{5}$;-$\frac{3}{5}$;$\frac{3}{5}$;-$\frac{3}{5}$.
点评 本题考查诱导公式的应用,考查计算能力.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
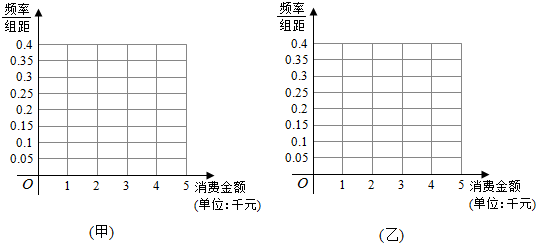
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 50 | 200 | 350 | 300 | 100 |
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 250 | 300 | 150 | 100 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com